练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    命题“对于任意角θ，cos4θ－sin4θ＝cos 2θ”的证明：cos4θ－sin4θ＝(cos2θ－sin2θ)(cos2θ＋sin2θ)＝cos2θ－sin2θ＝cos 2θ过程应用了(　　)

    A．分析法

    B．综合法

    C．综合法、分析法综合应用

    D．间接证明法


    B


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


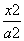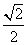    已知椭圆C：＋＝1(a>b>0)的一个顶点为A(2,0)，离心率为.直线y＝k(x－1)与椭圆C交于不同的两点M，N.

    (1)求椭圆C的方程；

    (2)当△AMN的面积为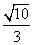时，求k的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    偶函数的图像关于直线对称，，则=________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    定义在上的奇函数,当≥0时,

    则关于的函数(0<<1)的所有零点之和为（　　）

    A、1-            B、               C、      D、

    查看答案和解析>>

    科目：高中数学 来源： 题型：


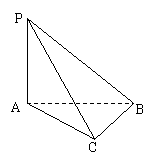
    三棱锥P−ABC中，PA⊥平面ABC，AB⊥BC。

    （１）证明：平面PAB⊥平面PBC；

    （２）若PA=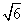，PC与侧面APB所成角的余弦值为，

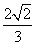    PB与底面ABC成60°角，

    求二面角B―PC―A的大小。

     


    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用反证法证明命题“若sin θ·＋cos θ·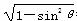＝1，则sin θ≥0且cos θ≥0”时，下列假设的结论正确的是(　　)

    A．sin θ≥0或cos θ≥0    B．sin θ<0且cos θ<0

    C．sin θ<0或cos θ<0      D．sin θ>0且cos θ>0

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝aln(1＋ex)－(a＋1)x(其中a>0)，点A(x1，f(x1))，B(x2，f(x2))，C(x3，f(x3))从左到右依次是函数y＝f(x)图象上三点，且2x2＝x1＋x3.

    (1)证明：函数f(x)在R上是减函数；

    (2)求证：△ABC是钝角三角形．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设a＝log32，b＝log52，c＝log23，则(　　)

    A．a>c>b             B．b>c>a   C．c>b>a             D．c>a>b

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝4x＋(x>0，a>0)在x＝3时取得最小值，则a＝________.

    查看答案和解析>>

    同步练习册答案