
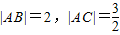 ,点A,B关于y轴对称.一曲线E过C点,动点P在曲线E上运动,且保持|PA|+|PB|的值不变.
,点A,B关于y轴对称.一曲线E过C点,动点P在曲线E上运动,且保持|PA|+|PB|的值不变.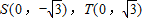 ,求∠SPT的最小值;
,求∠SPT的最小值;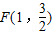 是曲线E上的一点,设M,N是曲线E上不同的两点,直线FM和FN的倾斜角互补,试判断直线MN的斜率是否为定值,如果是,求出这个定值;如果不是,请说明理由.
是曲线E上的一点,设M,N是曲线E上不同的两点,直线FM和FN的倾斜角互补,试判断直线MN的斜率是否为定值,如果是,求出这个定值;如果不是,请说明理由.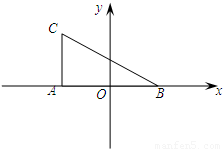
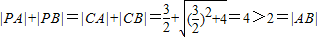 ,知动点P的轨迹为以A,B为焦点的椭圆,且
,知动点P的轨迹为以A,B为焦点的椭圆,且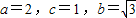 ,由此能求出曲线E的方程.
,由此能求出曲线E的方程.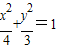 ,
,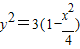 .由椭圆的对称性设点P在y轴右侧,即0<x≤2,则
.由椭圆的对称性设点P在y轴右侧,即0<x≤2,则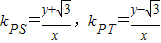 ,由到角公式得
,由到角公式得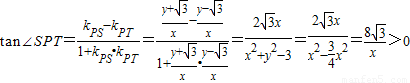 .由此能求出∠SPT的最小值.
.由此能求出∠SPT的最小值.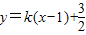 .由
.由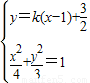 得(4k2+3)x2-4k(2k-3)x+4k2-12k-3=0.由此能够推导出直线MN的斜率为定值.
得(4k2+3)x2-4k(2k-3)x+4k2-12k-3=0.由此能够推导出直线MN的斜率为定值.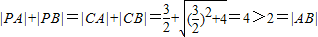 …(1分)
…(1分)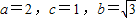 …(2分)
…(2分)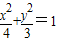 …(3分)
…(3分)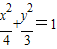 ,∴
,∴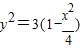
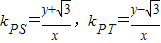 ,由到角公式得…(4分)
,由到角公式得…(4分)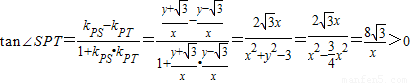
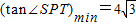 …(7分)
…(7分)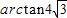 …(8分)
…(8分)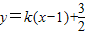
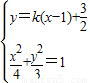 消y,整理得(4k2+3)x2-4k(2k-3)x+4k2-12k-3=0①…(10分)
消y,整理得(4k2+3)x2-4k(2k-3)x+4k2-12k-3=0①…(10分)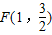 是直线FM与椭圆的交点,∴方程①的两根为1,x1
是直线FM与椭圆的交点,∴方程①的两根为1,x1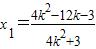 ②…(11分)
②…(11分)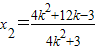 …(12分)
…(12分)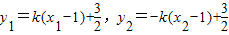 ∴
∴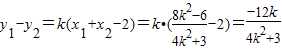
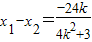 ,∴
,∴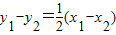
 …(14分)
…(14分)

 精英口算卡系列答案
精英口算卡系列答案科目:高中数学 来源: 题型:
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P.
如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P.查看答案和解析>>
科目:高中数学 来源: 题型:
 8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=
8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=
| ||
| 2 |
| DM |
| DN |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )
如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )A、(0,
| ||||
B、(
| ||||
C、(
| ||||
| D、(2,4] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com