
| A. | d>|OC|>2p | B. | d<|OC|<2p | C. | d=|OC|=2p | D. | d<|OC|=2p |
分析 设直线OA的方程为y=kx(k≠1,0),可得直线OB的方程为:y=-$\frac{1}{k}$x,直线方程分别与抛物线方程联立可得A,B的坐标.由直线AB的方程可得C(2p,0),D(p,0).设M(x0,y0),可得d=2$\sqrt{M{D}^{2}-{x}_{0}^{2}}$,即可得出结论.
解答 解:设直线OA的方程为y=kx(k≠1,0),则直线OB的方程为:y=-$\frac{1}{k}$x,
联立$\left\{\begin{array}{l}{y=kx}\\{{y}^{2}=2px}\end{array}\right.$,解得A$(\frac{2p}{{k}^{2}},\frac{2p}{k})$,同理可得B(2pk2,-2pk).
∴直线AB的方程为:y+2pk=$\frac{\frac{2p}{k}+2pk}{\frac{2p}{{k}^{2}}-2p{k}^{2}}$(x-2pk2),化为:y+2pk=$\frac{k}{1-{k}^{2}}$(x-2pk2),令y=0,解得x=2p,
∴C(2p,0),|OC|=2p.
D(p,0).
设M(x0,y0),
则d=2$\sqrt{M{D}^{2}-{x}_{0}^{2}}$=2$\sqrt{({x}_{0}-p)^{2}+{y}_{0}^{2}-{x}_{0}^{2}}$=2p.
综上可得:d=|OC|=2p.
故选:C.
点评 本题考查了抛物线的标准方程及其性质、直线与抛物线相交问题、直线与圆相交弦长问题、相互垂直的直线斜率之间的关系,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
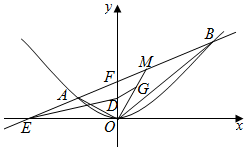 已知O是坐标系的原点,F是抛物线C:x2=4y的焦点,过点F的直线交抛物线于A,B两点,弦AB的中点为M,△OAB的重心为G.
已知O是坐标系的原点,F是抛物线C:x2=4y的焦点,过点F的直线交抛物线于A,B两点,弦AB的中点为M,△OAB的重心为G.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
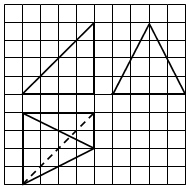 如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该多面体的体积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该多面体的体积为( )| A. | 48 | B. | 32 | C. | 16 | D. | $\frac{32}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | 在犯错误的概率不超过0.1%的前提下,认为“爱好运动与性别有关” | |
| B. | 有99%以上的把握认为“爱好运动与性别有关” | |
| C. | 在犯错误的概率不超过0.1%的前提下,认为“爱好运动与性别无关” | |
| D. | 有99%以上的把握认为“爱好运动与性别无关” |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com