
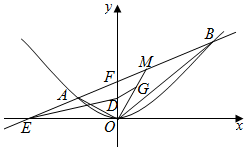
 已知O是坐标系的原点,F是抛物线C:x2=4y的焦点,过点F的直线交抛物线于A,B两点,弦AB的中点为M,△OAB的重心为G.
已知O是坐标系的原点,F是抛物线C:x2=4y的焦点,过点F的直线交抛物线于A,B两点,弦AB的中点为M,△OAB的重心为G.分析 (Ⅰ)求得焦点F(0,1),显然直线AB的斜率存在,设AB:y=kx+1,代入抛物线的方程,运用韦达定理和三角形的重心坐标,运用代入法消去k,即可得到所求轨迹方程;
(Ⅱ)求得D,E和G的坐标,|DG|和|ME|的长,以及D点到直线AB的距离,运用四边形的面积公式,结合基本不等式可得最小值,由等号成立的条件,可得直线AB的方程.
解答  解:(Ⅰ)焦点F(0,1),显然直线AB的斜率存在,
解:(Ⅰ)焦点F(0,1),显然直线AB的斜率存在,
设AB:y=kx+1,
联立x2=4y,消去y得,x2-4kx-4=0,
设A(x1,y1),B(x2,y2),G(x,y),
则x1+x2=4k,x1x2=-4,
所以${y_1}+{y_2}=k{x_1}+1+k{x_2}+1=4{k^2}+2$,
所以$\left\{{\begin{array}{l}{x=\frac{4k}{3}}\\{y=\frac{{4{k^2}+2}}{3}}\end{array}}\right.$,
消去k,得重心G的轨迹方程为$y=\frac{3}{4}{x^2}+\frac{2}{3}$;
(Ⅱ)由已知及(Ⅰ)知,$D(0,\frac{2}{3}),E(-\frac{1}{k},0),k≠0,{x_M}=2k,{x_G}=\frac{4k}{3}$,
因为$\frac{{|{OD}|}}{{|{OF}|}}=\frac{2}{3}=\frac{{|{OG}|}}{{|{OM}|}}$,所以DG∥ME,(注:也可根据斜率相等得到),$|{DG}|=\sqrt{1+{k^2}}|{\frac{4k}{3}}|,|{ME}|=\sqrt{1+{k^2}}|{2k-(-\frac{1}{k})}|=\sqrt{1+{k^2}}(2|k|+|{\frac{1}{k}}|)$,
D点到直线AB的距离$d=\frac{{\frac{1}{3}}}{{\sqrt{1+{k^2}}}}=\frac{1}{{3\sqrt{1+{k^2}}}}$,
所以四边形DEMG的面积$S=\frac{1}{2}\sqrt{1+{k^2}}•(|{\frac{4k}{3}}|+2|k|+|{\frac{1}{k}}|)•\frac{1}{{3\sqrt{1+{k^2}}}}=\frac{1}{6}(\frac{10}{3}|k|+\frac{1}{|k|})≥\frac{1}{6}•2\sqrt{\frac{10}{3}}=\frac{{\sqrt{30}}}{9}$,
当且仅当$\frac{10}{3}|k|=\frac{1}{|k|}$,即$k=±\frac{{\sqrt{30}}}{10}$时取等号,
此时四边形DEMG的面积最小,
所求的直线AB的方程为$y=±\frac{{\sqrt{30}}}{10}x+1$.
点评 本题考查轨迹方程的求法,注意运用代入法,考查四边形面积的最值的求法,注意运用弦长公式和点到直线的距离和基本不等式,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
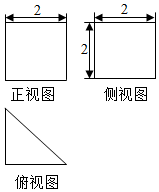
| A. | 1:3π | B. | $\sqrt{3}:π$ | C. | $1:3\sqrt{3}π$ | D. | $1:\sqrt{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{10}$ | B. | 2$\sqrt{10}$ | C. | $\sqrt{5}$ | D. | 2$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{2}{3}$ | B. | $-\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | d>|OC|>2p | B. | d<|OC|<2p | C. | d=|OC|=2p | D. | d<|OC|=2p |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com