
分析 (1)求得抛物线的焦点和准线方程,根据抛物线的定义,即可得到所求|MF|;
(2)假设存在点N,使得以PQ为直径的圆恒过点N,由直线l2:y=kx+m与抛物线C有唯一公共点P知,直线l2与抛物线C相切,利用导数求出直线l2的方程,进而求出Q点坐标,根据直径所对的圆周角为直角,利用$\overrightarrow{NP}$•$\overrightarrow{NQ}$=0,求出N点坐标.
解答 解:(1)抛物线C的方程为x2=4y的焦点坐标为F(0,1),准线方程为y=-1,
由抛物线的定义可得|MF|=1+1=2;
(2)由抛物线C关于y轴对称可知,若存在点N,使得以PQ为直径的圆恒过点N,
则点N必在y轴上,设N(0,n),
又设点P(x0,$\frac{{{x}_{0}}^{2}}{4}$),
由直线l2:y=kx+m与抛物线C有唯一公共点P知,直线l与抛物线C相切,
由y=$\frac{1}{4}$x2得y′=$\frac{1}{2}$x,可得直线l2的斜率为$\frac{1}{2}$x0,
可得直线l的方程为y-$\frac{{{x}_{0}}^{2}}{4}$=$\frac{1}{2}$x0(x-x0),
令y=-1得x=$\frac{{x}_{0}}{2}$-$\frac{2}{{x}_{0}}$,
可得Q点的坐标为($\frac{{x}_{0}}{2}$-$\frac{2}{{x}_{0}}$,-1),
即有$\overrightarrow{NP}$=(x0,$\frac{{{x}_{0}}^{2}}{4}$-n),$\overrightarrow{NQ}$=($\frac{{x}_{0}}{2}$-$\frac{2}{{x}_{0}}$,-1-n),
由点N在以PQ为直径的圆上,
可得$\overrightarrow{NP}$•$\overrightarrow{NQ}$=$\frac{{{x}_{0}}^{2}}{2}$-(1+n)($\frac{{{x}_{0}}^{2}}{4}$-n)=(1-n)•$\frac{{{x}_{0}}^{2}}{4}$+n2+n-2=0,(*)
要使方程(*)对x0恒成立,必须有$\left\{\begin{array}{l}{1-n=0}\\{{n}^{2}+n-2=0}\end{array}\right.$,解得n=1,
则在坐标平面内存在点N,使得以PQ为直径的圆恒过点N,其坐标为(0,1).
点评 本题考查了抛物线的定义及直线与抛物线的位置关系,这类题目考查比较灵活,解决问题时注意几何关系向代数关系(即坐标关系)的转化.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2=py(x≠0) | B. | y2=px(y≠0) | C. | x2=4py(x≠0) | D. | y2=4px(y≠0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
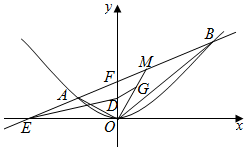 已知O是坐标系的原点,F是抛物线C:x2=4y的焦点,过点F的直线交抛物线于A,B两点,弦AB的中点为M,△OAB的重心为G.
已知O是坐标系的原点,F是抛物线C:x2=4y的焦点,过点F的直线交抛物线于A,B两点,弦AB的中点为M,△OAB的重心为G.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com