
分析 (1)设出直线PQ的方程,与抛物线方程联立消去y,根据韦达定理求得x1x2的值,由抛物线的定义分别表示出|FP|,|FQ|,代入$\frac{1}{FP}+\frac{1}{FQ}$整理得到定值,最后验证斜率不存在时的情况;
(2)设出直线PQ的方程,联立抛物线方程,运用韦达定理和两点的距离公式,化简整理,即可求得定点M和定值;
(3)运用向量共线的坐标表示和向量垂直的条件,化简整理即可求得定点N.
解答 解:(1)证明:抛物线的焦点为F(1,0),
设直线PQ的方程为y=k(x-1)(k≠0),
代入抛物线方程,消去y,得k2x2-2(k2+2)x+k2=0,
由根与系数的关系,得x1x2=1,x1+x2=2+$\frac{4}{{k}^{2}}$,
由抛物线的定义,知|FP|=x1+1,|FQ|=x2+1.
$\frac{1}{FP}+\frac{1}{FQ}$=$\frac{1}{{x}_{1}+1}$+$\frac{1}{{x}_{2}+1}$
=$\frac{{x}_{1}+{x}_{2}+2}{{x}_{1}{x}_{2}+({x}_{1}+{x}_{2})+1}$=$\frac{2+\frac{4}{{k}^{2}}+2}{1+2+\frac{4}{{k}^{2}}+1}$=1为定值.
当PQ⊥x轴时,|FP|=|FQ|=2,上式仍成立;
(2)证明:设M(m,0),当PQ⊥x轴时,令x=m,可得y2=4m,
|MP|=|MQ|=2$\sqrt{m}$,有$\frac{1}{{M{P^2}}}+\frac{1}{{M{Q^2}}}$为定值$\frac{1}{2m}$.
当PQ斜率存在时,设PQ:x=ty+m,代入抛物线方程可得,
y2-4ty-4m=0,设P($\frac{{{y}_{1}}^{2}}{4}$,y1),Q($\frac{{{y}_{2}}^{2}}{4}$,y2),
则y1+y2=4t,y1y2=-4m.
即有|MP|2=(m-$\frac{{{y}_{1}}^{2}}{4}$)2+y12=$\frac{(-{y}_{1}{y}_{2}-{{y}_{1}}^{2})^{2}}{16}$+y12=(1+t2)y12,
同理|MQ|2=(m-$\frac{{{y}_{2}}^{2}}{4}$)2+y22=(1+t2)y22.
即有$\frac{1}{{M{P^2}}}+\frac{1}{{M{Q^2}}}$=$\frac{1}{1+{t}^{2}}$•$\frac{16{t}^{2}+8m}{16{m}^{2}}$,
存在m=2即有定点M(2,0)时,上式为$\frac{1}{1+{t}^{2}}$•$\frac{16(1+{t}^{2})}{64}$=$\frac{1}{4}$为定值;
(3)$\overrightarrow{PM}=λ\overrightarrow{MQ}$,可得$\overrightarrow{NM}$=$\frac{\overrightarrow{NP}+λ\overrightarrow{NQ}}{1+λ}$,
$\overrightarrow{NM}⊥({\overrightarrow{NP}-λ\overrightarrow{NQ}})$,可得($\overrightarrow{NP}$+λ$\overrightarrow{NQ}$)•($\overrightarrow{NP}$-λ$\overrightarrow{NQ}$)=0,
即为NP2=λ2NQ2,
由P($\frac{{{y}_{1}}^{2}}{4}$,y1),Q($\frac{{{y}_{2}}^{2}}{4}$,y2),M(2,0),
设$\overrightarrow{PM}$=λ$\overrightarrow{MQ}$,
则y1=-λy2,①2-$\frac{{{y}_{1}}^{2}}{4}$=λ($\frac{{{y}_{2}}^{2}}{4}$-2),②
又设N(n,0)(n<0),则(n-$\frac{{{y}_{1}}^{2}}{4}$)2+y12=λ2[($\frac{{{y}_{2}}^{2}}{4}$-n)2+y22],
即为$\frac{{{y}_{1}}^{2}}{4}$-n=λ($\frac{{{y}_{2}}^{2}}{4}$-n),③
将①平方可得,y12=λ2y22,④,
将④代入②③,化简可得n=-2.
则N(-2,0).
点评 本题主要考查了抛物线的简单性质,直线与抛物线的关系.同时考查向量垂直的条件和向量共线的坐标表示,注意运用韦达定理和抛物线的定义是解题的关键,具有一定的运算量,属于中档题.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2=py(x≠0) | B. | y2=px(y≠0) | C. | x2=4py(x≠0) | D. | y2=4px(y≠0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,网格纸上正方形小格的边长为1,图中粗线画出的是某四棱锥的三视图,则该四棱锥的四个侧面中面积最小的一个侧面的面积为( )
如图,网格纸上正方形小格的边长为1,图中粗线画出的是某四棱锥的三视图,则该四棱锥的四个侧面中面积最小的一个侧面的面积为( )| A. | 4 | B. | 4$\sqrt{6}$ | C. | 8 | D. | 8$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
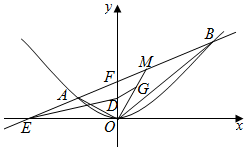 已知O是坐标系的原点,F是抛物线C:x2=4y的焦点,过点F的直线交抛物线于A,B两点,弦AB的中点为M,△OAB的重心为G.
已知O是坐标系的原点,F是抛物线C:x2=4y的焦点,过点F的直线交抛物线于A,B两点,弦AB的中点为M,△OAB的重心为G.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{4}$ | B. | 向右平移$\frac{π}{4}$ | C. | 向右平移$\frac{π}{8}$ | D. | 向左平移$\frac{π}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com