
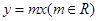 与函数
与函数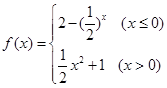 的图象恰好有三个不同的公共点,则实数
的图象恰好有三个不同的公共点,则实数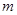 的取值范围是 .
的取值范围是 . 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源:不详 题型:解答题
 m,盖子边长为
m,盖子边长为 m,
m,
 关于
关于 的解析式;
的解析式;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 时,排水量V是垃圾杂物密度x的一次函数。
时,排水量V是垃圾杂物密度x的一次函数。 时,求函数V(x)的表达式;
时,求函数V(x)的表达式; 可以达到最大,求出这个最大值。
可以达到最大,求出这个最大值。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
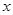 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为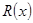 万元,且
万元,且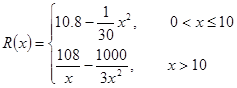 .
.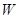 (万元)关于年产量
(万元)关于年产量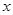 (千件)的函数解析式;
(千件)的函数解析式; 查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
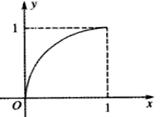
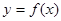 图象如图所示,对于满足0<
图象如图所示,对于满足0<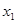 <
<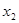 <1的
<1的 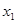 ,
,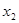 给出下列结论:
给出下列结论: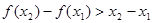 ②
②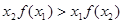 ③
③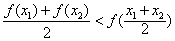 ;
;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com