
【题目】某次乒乓球比赛的决赛在甲乙两名选手之间举行,比赛采用五局三胜制,按以往比赛经验,甲胜乙的概率为![]() .
.
(Ⅰ)求比赛三局甲获胜的概率;
(Ⅱ)求甲获胜的概率;
(Ⅲ)设甲比赛的次数为![]() ,求
,求![]() 的数学期望.
的数学期望.
科目:高中数学 来源: 题型:
【题目】分别根据下列条件,求圆的方程:
(1)过两点(0,4),(4,6),且圆心在直线x﹣2y﹣2=0上;
(2)半径为 ![]() ,且与直线2x+3y﹣10=0切于点(2,2).
,且与直线2x+3y﹣10=0切于点(2,2).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机床厂今年初用98万元购进一台数控机床,并立即投入使用,计划第一年维修、保养费用12万元,从第二年开始,每年的维修、保养修费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利总额y元.
(1)写出y与x之间的函数关系式;
(2)从第几年开始,该机床开始盈利?
(3)使用若干年后,对机床的处理有两种方案:①当年平均盈利额达到最大值时,以30万元价格处理该机床;②当盈利额达到最大值时,以12万元价格处理该机床.问哪种方案处理较为合理?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,对任意的正整数n,都有Sn=![]() an+n﹣3成立.
an+n﹣3成立.
(Ⅰ)求证:{an﹣1}为等比数列;
(Ⅱ)求数列{nan}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从盛满2升纯酒精的容器里倒出1升,然后加满水,再倒出1升混合溶液后又用水填满,以此继续下去,则至少应倒次后才能使纯酒精体积与总溶液的体积之比低于10%.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班20名同学某次数学测试的成绩可绘制成如下茎叶图,由于其中部分数据缺失,故打算根据茎叶图中的数据估计全班同学的平均成绩.
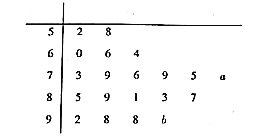
(1)完成频率分布直方图;
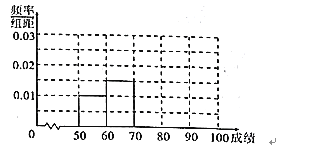
(2)根据(1)中的频率分布直方图估计全班同学的平均成绩![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(3)设根据茎叶图计算出的全班的平均成绩为![]() ,并假设
,并假设![]() ,且
,且![]() 各自取得每一个可能值的机会相等,在(2)的条件下,求概率
各自取得每一个可能值的机会相等,在(2)的条件下,求概率![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线;
处的切线;
(2)若函数![]() 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,若在
,若在![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是边长2的正方形,E,F分别为线段DD1 , BD的中点. 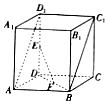
(1)求证:EF∥平面ABC1D1;
(2)AA1=2 ![]() ,求异面直线EF与BC所成的角的大小.
,求异面直线EF与BC所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的左右焦点,
的左右焦点,![]() 为原点,
为原点,![]()
![]() 在椭圆上,线段
在椭圆上,线段![]() 与
与![]() 轴的交点
轴的交点![]() 满足
满足![]() .
.
(1)求椭圆的标准方程;
(2)过椭圆右焦点![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,若
点,若![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com