
【题目】已知函数![]() (
(![]() ).
).
(1)求函数![]() 的单调区间;
的单调区间;
(2)函数![]() 在定义域内存在零点,求
在定义域内存在零点,求![]() 的取值范围.
的取值范围.
(3)若![]() ,当
,当![]() 时,不等式
时,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围
的取值范围
【答案】(1)当![]() 时,函数
时,函数![]() 的单调增区间为
的单调增区间为![]() ,当
,当![]() 时,函数
时,函数![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)先求函数的导数,分![]() 和
和![]() 求函数的单调区间;(2)将
求函数的单调区间;(2)将![]() 的零点问题,转化
的零点问题,转化
为![]() ,
,![]() 的问题,所以设函数
的问题,所以设函数![]()
![]() (
(![]() ),求函数的导数,在定义域内分析函数的单调区间,根据单调性和极值点得到函数的最小值,然后再根据函数的变化速度分析函数没有最大值,趋于正无穷大;(3)由(2)知,当
),求函数的导数,在定义域内分析函数的单调区间,根据单调性和极值点得到函数的最小值,然后再根据函数的变化速度分析函数没有最大值,趋于正无穷大;(3)由(2)知,当![]() 时,
时,![]() ,即
,即![]() ,
,![]() ,先分析法证明:
,先分析法证明:![]() ,
,![]() .根据
.根据![]() ,将问题转化为证明
,将问题转化为证明![]() ,然后结合(1)所讨论的单调区间,求得满足条件的
,然后结合(1)所讨论的单调区间,求得满足条件的![]() 的取值范围.
的取值范围.
试题解析:(1)由![]() ,则
,则![]() .
.
当![]() 时,对
时,对![]() ,有
,有![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上单调递增;
上单调递增;
当![]() 时,由
时,由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() ,
,
此时函数![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
综上所述,当![]() 时,函数
时,函数![]() 的单调增区间为
的单调增区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
(2)函数![]() 的定义域为
的定义域为![]() ,
,
由![]() ,得
,得![]() (
(![]() )
)
令![]()
![]() (
(![]() ),则
),则![]()
![]() ,
,
由于![]() ,
,![]() ,可知当
,可知当![]() ,
,![]() ;当
;当![]() 时,
时,![]() ,
,
故函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,故
上单调递增,故![]() .
.
又由(1)知当![]() 时,对
时,对![]() ,有
,有![]() ,即
,即![]() ,
,
(随着![]() 的增长,
的增长,![]() 的增长速度越来越快,会超过并远远大于
的增长速度越来越快,会超过并远远大于![]() 的增长速度,而
的增长速度,而![]() 的增长速度则会越来越慢.则当
的增长速度则会越来越慢.则当![]() 且
且![]() 无限接近于0时,
无限接近于0时,![]() 趋向于正无穷大.)
趋向于正无穷大.)
∴当![]() 时,函数
时,函数![]() 有零点;
有零点;
(3)由(2)知,当![]() 时,
时,![]() ,即
,即![]() .
.
先分析法证明:![]() .
.
要证![]() 只需证明
只需证明![]() 即证
即证![]()
设![]() ,则
,则![]()
所以![]() 在
在![]() 时函数单调递增,所以
时函数单调递增,所以![]() ,则
,则![]()
当![]() 时,由(1)知,函数
时,由(1)知,函数![]() 在
在![]() 单调递增,则
单调递增,则![]() 在
在![]() 恒成立;
恒成立;
当![]() 时,由(1)知,函数
时,由(1)知,函数![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减.故当
单调递减.故当![]() 时
时![]() ,所以
,所以![]() ,则不满足题意,舍去.
,则不满足题意,舍去.
综上,满足题意的实数a的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知正方形![]() 的边长为1,如图所示:
的边长为1,如图所示:
(1)在正方形内任取一点![]() ,求事件“
,求事件“![]() ”的概率;
”的概率;
(2)用芝麻颗粒将正方形均匀铺满,经清点,发现芝麻一共56粒,有44粒落在扇形![]() 内,请据此估计圆周率
内,请据此估计圆周率![]() 的近似值(精确到0.001).
的近似值(精确到0.001).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设小明订了一份报纸,送报人可能在早上6:30—7:30之间把报纸送到,小明离家的时间在早上7:00—8:00之间,则他在离开家之前能拿到报纸的概率( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的定义域为
的定义域为![]() ,若存在闭区间[m,n]
,若存在闭区间[m,n] ![]() D,使得函数
D,使得函数![]() 满足:①
满足:①![]() 在[m,n]上是单调函数;②
在[m,n]上是单调函数;②![]() 在[m,n]上的值域为[2m,2n],则称区间[m,n]为
在[m,n]上的值域为[2m,2n],则称区间[m,n]为![]() 的“倍值区间”.下列函数中存在“倍值区间”的有 .(填上所有正确的序号)
的“倍值区间”.下列函数中存在“倍值区间”的有 .(填上所有正确的序号)
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果y=f(x)的定义域为R,对于定义域内的任意x,存在实数a使得f(x+a)=f(﹣x)成立,则称此函数具有“P(a)性质”.给出下列命题:
①函数y=sinx具有“P(a)性质”;
②若奇函数y=f(x)具有“P(2)性质”,且f(1)=1,则f(2015)=1;
③若函数y=f(x)具有“P(4)性质”,图象关于点(1,0)成中心对称,且在(﹣1,0)上单调递减,则y=f(x)在(﹣2,﹣1)上单调递减,在(1,2)上单调递增;
④若不恒为零的函数y=f(x)同时具有“P(0)性质”和“P(3)性质”,函数y=f(x)是周期函数.
其中正确的是 (写出所有正确命题的编号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,椭圆
,椭圆![]() 过点
过点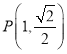 ,直线
,直线![]() 交
交![]() 轴于
轴于![]() ,且
,且![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 的上顶点,过点
的上顶点,过点![]() 分别作直线
分别作直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为![]() ,且
,且![]() ,证明:直线
,证明:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD-A1B1C1D中,S是B1D1的中点,E、F、G分别是BC、CD和SC的中点.求证:
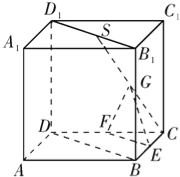
(1)直线EG∥平面BDD1B1;
(2)平面EFG∥平面BDD1B1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com