
【题目】函数![]() 的定义域为
的定义域为![]() ,若存在闭区间[m,n]
,若存在闭区间[m,n] ![]() D,使得函数
D,使得函数![]() 满足:①
满足:①![]() 在[m,n]上是单调函数;②
在[m,n]上是单调函数;②![]() 在[m,n]上的值域为[2m,2n],则称区间[m,n]为
在[m,n]上的值域为[2m,2n],则称区间[m,n]为![]() 的“倍值区间”.下列函数中存在“倍值区间”的有 .(填上所有正确的序号)
的“倍值区间”.下列函数中存在“倍值区间”的有 .(填上所有正确的序号)
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() .
.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某超市经营一批产品,在市场销售中发现此产品在30天内的日销售量P(件)与日期![]() )之间满足
)之间满足![]() ,已知第5日的销售量为55件,第10日的销售量为50件。
,已知第5日的销售量为55件,第10日的销售量为50件。
(1)求第20日的销售量; (2)若销售单价Q(元/件)与![]() 的关系式为
的关系式为![]() ,求日销售额
,求日销售额![]() 的最大值。
的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第![]() 届夏季奥林匹克运动会2016年8月5日到2016年8月21日在巴西里约热内卢举行,为了解我校学生“收看奥运会足球赛”是否与性別有关,从全校学生中随机抽取
届夏季奥林匹克运动会2016年8月5日到2016年8月21日在巴西里约热内卢举行,为了解我校学生“收看奥运会足球赛”是否与性別有关,从全校学生中随机抽取![]() 名进行了问卷调查,得到
名进行了问卷调查,得到![]() 列联表,从这
列联表,从这![]() 名同学中随机抽取
名同学中随机抽取![]() 人,抽到“收看奥运会足球赛 ”的学生的概率是
人,抽到“收看奥运会足球赛 ”的学生的概率是![]() .
.
男生 | 女生 | 合计 | |
收看 |
| ||
不收看 |
| ||
合计 |
|
(1)请将上面的![]() 列联表补充完整,并据此资料分析“收看奥运会足球赛”与性別是否有关;
列联表补充完整,并据此资料分析“收看奥运会足球赛”与性別是否有关;
(2)若从这![]() 名同学中的男同学中随机抽取
名同学中的男同学中随机抽取![]() 人参加有奖竞猜活动,记抽到收看奥运会足球赛”的学生人数为
人参加有奖竞猜活动,记抽到收看奥运会足球赛”的学生人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式:
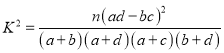 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ,第五组
,第五组![]() ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.
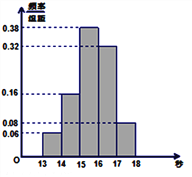
(1)若成绩小于15秒认为良好,求该样本在这次百米测试中成绩良好的人数;
(2)请估计学校1800名学生中,成绩属于第四组的人数;
(3)请根据频率分布直方图,求样本数据的众数、中位数、平均数和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中, 以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系, 已知点
轴的非负半轴为极轴建立极坐标系, 已知点![]() 的极坐标为
的极坐标为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() 为参数).
为参数).
(1)直线![]() 过
过![]() 且与曲线
且与曲线![]() 相切, 求直线
相切, 求直线![]() 的极坐标方程;
的极坐标方程;
(2)点![]() 与点
与点![]() 关于
关于![]() 轴对称, 求曲线
轴对称, 求曲线![]() 上的点到点
上的点到点![]() 的距离的取值范围.
的距离的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com