
【题目】已知函数![]() .(Ⅰ)求函数
.(Ⅰ)求函数![]() 的最小正周期及单调递增区间;(Ⅱ)将
的最小正周期及单调递增区间;(Ⅱ)将![]() 的图像向右平移
的图像向右平移![]() 个单位得到函数
个单位得到函数![]() 的图像,若
的图像,若![]() ,求函数
,求函数![]() 的值域.
的值域.
【答案】(Ⅰ)![]() .单调递增区间为[-
.单调递增区间为[-![]() +k
+k![]() ,
, ![]() +k
+k![]() ],
], ![]() ; (Ⅱ)
; (Ⅱ)![]() .
.
【解析】试题分析:(1)首先通过三角函数的恒等变换,把三角函数的关系式变形成正弦型函数,进一步利用三角函数的性质求出函数的周期和单调区间;(2)利用上步的结论,进一步利用函数的定义域求出三角函数的值域.
试题解析:
(Ⅰ)f(x)=cos x(![]() sin x+cos x)+1
sin x+cos x)+1
=cos2x+![]() sin x cos x+1
sin x cos x+1![]()
=![]() cos2x+
cos2x+![]() sin2x+
sin2x+![]()
=sin(2x+![]() )+
)+![]()
∵T=![]() =
=![]() =
= ![]()
即函数f(x)的最小正周期为![]() .
.
由f(x)=sin(2x+![]() )+
)+![]()
由2k![]() -
-![]() ≤2x+
≤2x+![]() ≤2k
≤2k![]() +
+![]() ,
, ![]()
解得:-![]() +k
+k![]() ≤x≤
≤x≤![]() +k
+k![]() ,
, ![]()
故函数f(x)=sin(2x+![]() )+
)+![]() 的单调递增区间为[-
的单调递增区间为[-![]() +k
+k![]() ,
, ![]() +k
+k![]() ],
], ![]() .
.
(Ⅱ)![]() ,x
,x![]() [-
[-![]() ,
,![]() ],-
],- ![]() ≤2x≤
≤2x≤![]() ,
,
∴-![]() ≤
≤![]() ≤1
≤1
∴函数的值域为![]() .
.


科目:高中数学 来源: 题型:
【题目】函数![]() 的定义域为
的定义域为![]() ,若存在闭区间[m,n]
,若存在闭区间[m,n] ![]() D,使得函数
D,使得函数![]() 满足:①
满足:①![]() 在[m,n]上是单调函数;②
在[m,n]上是单调函数;②![]() 在[m,n]上的值域为[2m,2n],则称区间[m,n]为
在[m,n]上的值域为[2m,2n],则称区间[m,n]为![]() 的“倍值区间”.下列函数中存在“倍值区间”的有 .(填上所有正确的序号)
的“倍值区间”.下列函数中存在“倍值区间”的有 .(填上所有正确的序号)
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,椭圆
,椭圆![]() 过点
过点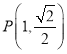 ,直线
,直线![]() 交
交![]() 轴于
轴于![]() ,且
,且![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 的上顶点,过点
的上顶点,过点![]() 分别作直线
分别作直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为![]() ,且
,且![]() ,证明:直线
,证明:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某书店销售刚刚上市的某知名品牌的高三数学单元卷,按事先拟定的价格进行![]() 天试销,每种单价试销
天试销,每种单价试销![]() 天,得到如下数据:
天,得到如下数据:
单价 |
|
|
|
|
|
销量 |
|
|
|
|
|
(1)求试销![]() 天的销量的方差和
天的销量的方差和![]() 对
对![]() 的回归直线方程;
的回归直线方程;
(2)预计今后的销售中,销量与单价服从(1)中的回归方程,已知每册单元卷的成本是![]() 元,
元,
为了获得最大利润,该单元卷的单价应定为多少元?
附:  ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解高中生上学使用手机情况,调查者进行了如下的随机调查:调查者向被调查者提出两个问题:(1)你的学号是奇数吗?(2)你上学时是否经常带手机?要求被调查者背对着调查人员抛掷一枚硬币,如果出现正面,就回答第一问题,否则就回答第二个问题.被调查者不必告诉调查人员自己回答的是哪一个问题,只需回答“是”或“不是”,因为只有被调查者本人知道回答了哪一个问题,所以都如实地做了回答.结果被调查的800人(学号从1至800)中有260人回答了“是”.由此可以估计这800人中经常带手机上学的人数是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com