解:(1)∵函数f(x)=x
3-3x
2+3x,∴f′(x)=3x
2 -6x+3,∴f″(x)=6x-6.
令 f″(x)=6x-6=0,解得 x=1,且f(1)=1,故函数f(x)=x
3-3x
2+3x对称中心为(1,1),
故答案为 (1,1).
(2)若函数g(x)=

x
3-

x
2+3x-

+

=

x
3-

x
2+3x-

+

,令h(x)=

x
3-

x
2+3x-

,m(x)=

,则g(x)=h(x)+m(x).
则h′(x)=x
2-x+3,h″(x)=2x-1,令h″(x)=0,可得x=

,故h(x)的对称中心为(

,1).
设点p(x
0,y
0)为曲线上任意一点,则点P关于(

,1)的对称点P′(1-x
0,2-y
0)也在曲线上,
∴h(1-x
0)=2-y
0 ,∴h(x
0)+h(1-x
0)=y
0+(2-y
0)=2.
∴h(

)+h(

)+h(
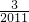
)+h(
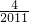
)+…+h(

)
=[h(

)+h(

)]+[h(

)+h(

)]+[h(
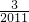
)+h(
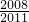
)]+…+[h(
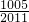
)+h(
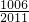
)]=1005×2=2010.
由于函数m(x)=

的对称中心为(

,0),可得m(x
0)+m(1-x
0)=0.
∴m(

)+m(

)+m(
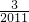
)+m(
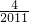
)+…+m(

)
=[m(

)+m(

)]+[m(

)+m(

)]+[m(
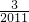
)+m(
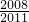
)]+…+[m(
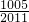
)+m(
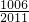
)]=1005×0=0.
∴g(

)+g(

)+g(
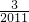
)+g(
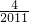
)+…+g(

)=h(

)+h(

)+h(
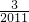
)+h(
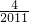
)+…+h(

)
+m(

)+m(

)+m(
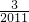
)+m(
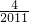
)+…+m(

)
=2010+0=2010,
故答案为2010.
分析:(1)根据函数f(x)的解析式求出f′(x)和f″(x),令f″(x)=0,求得x的值,由此求得函数f(x)=x
3-3x
2+3x对称中心.
(2)令h(x)=

x
3-

x
2+3x-

,m(x)=

,则g(x)=h(x)+m(x).利用对称性求得h(

)+h(

)+h(
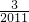
)+h(
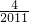
)+…+h(

)=2010,求得m(

)+m(

)+m(
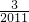
)+m(
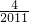
)+…+m(

)=0,从而求得g(x)=h(x)+m(x)的值.
点评:本小题主要考查函数与导数等知识,考查化归与转化的数学思想方法,考查化简计算能力,求函数的值以及函数的对称性的应用,属于难题.

 x3-
x3- x2+3x-
x2+3x- +
+ ,则g(
,则g( )+g(
)+g( )+g(
)+g(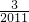 )+g(
)+g(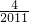 )+…+g(
)+…+g( )=________.
)=________. x3-
x3- x2+3x-
x2+3x- +
+ =
= x3-
x3- x2+3x-
x2+3x- +
+ ,令h(x)=
,令h(x)= x3-
x3- x2+3x-
x2+3x- ,m(x)=
,m(x)= ,则g(x)=h(x)+m(x).
,则g(x)=h(x)+m(x). ,故h(x)的对称中心为(
,故h(x)的对称中心为( ,1).
,1). ,1)的对称点P′(1-x0,2-y0)也在曲线上,
,1)的对称点P′(1-x0,2-y0)也在曲线上, )+h(
)+h( )+h(
)+h(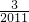 )+h(
)+h(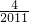 )+…+h(
)+…+h( )
) )+h(
)+h( )]+[h(
)]+[h( )+h(
)+h( )]+[h(
)]+[h(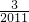 )+h(
)+h(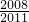 )]+…+[h(
)]+…+[h(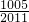 )+h(
)+h(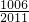 )]=1005×2=2010.
)]=1005×2=2010. 的对称中心为(
的对称中心为( ,0),可得m(x0)+m(1-x0)=0.
,0),可得m(x0)+m(1-x0)=0. )+m(
)+m( )+m(
)+m(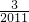 )+m(
)+m(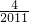 )+…+m(
)+…+m( )
) )+m(
)+m( )]+[m(
)]+[m( )+m(
)+m( )]+[m(
)]+[m(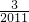 )+m(
)+m(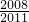 )]+…+[m(
)]+…+[m(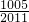 )+m(
)+m(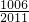 )]=1005×0=0.
)]=1005×0=0. )+g(
)+g( )+g(
)+g(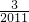 )+g(
)+g(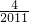 )+…+g(
)+…+g( )=h(
)=h( )+h(
)+h( )+h(
)+h(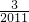 )+h(
)+h(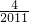 )+…+h(
)+…+h( )
) )+m(
)+m( )+m(
)+m(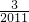 )+m(
)+m(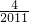 )+…+m(
)+…+m( )
) x3-
x3- x2+3x-
x2+3x- ,m(x)=
,m(x)= ,则g(x)=h(x)+m(x).利用对称性求得h(
,则g(x)=h(x)+m(x).利用对称性求得h( )+h(
)+h( )+h(
)+h(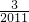 )+h(
)+h(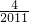 )+…+h(
)+…+h( )=2010,求得m(
)=2010,求得m( )+m(
)+m( )+m(
)+m(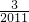 )+m(
)+m(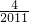 )+…+m(
)+…+m( )=0,从而求得g(x)=h(x)+m(x)的值.
)=0,从而求得g(x)=h(x)+m(x)的值.
