
����Ŀ��ij��ͧ���쳧�з���һ������ͧ������ǰ5���µIJ������£�

��1����![]() ����
����![]() �Ļع�ֱ�߷���Ϊ
�Ļع�ֱ�߷���Ϊ![]() �ָ��ݱ��������Ѿ���ȷ�������
�ָ��ݱ��������Ѿ���ȷ�������![]() ��ֵΪ
��ֵΪ![]() ������
������![]() ��ֵ�������Ƹó�
��ֵ�������Ƹó�![]() �·ݵIJ���������������ȷ��
�·ݵIJ���������������ȷ��![]() ��
��
�����ʼ첿�ŷ��ָó�![]() �·���������ͧ�������������⣬Ҫ���ٻأ�����һ���ι�˾����ó������˽���ǰ��������������ͧ
�·���������ͧ�������������⣬Ҫ���ٻأ�����һ���ι�˾����ó������˽���ǰ��������������ͧ![]() �ң�������ι�˾����ͧ���ٻصĸ���.
�ң�������ι�˾����ͧ���ٻصĸ���.
���𰸡�(��)�𰸼�������(��)![]() .
.
��������������(��)���ݱ������![]() ��ƽ��ֵ������ع鷽�̼������
��ƽ��ֵ������ع鷽�̼������![]() ��ֵ������������ó�
��ֵ������������ó�![]() �·ݵIJ�����(��)������������һ�����·���ͧ��ţ�Ȼ���оٳ����ܵĽ�������ҳ�����Ҫ�����ϣ���������¼��ĸ���.
�·ݵIJ�����(��)������������һ�����·���ͧ��ţ�Ȼ���оٳ����ܵĽ�������ҳ�����Ҫ�����ϣ���������¼��ĸ���.
��⣺(1��![]()
��Ϊ�ع�ֱ��![]() ����
����![]() ����
����![]()
����![]() ��
��![]() ʱ��
ʱ��![]()
���Թ��Ƹó�![]() �·ݵIJ���Ϊ
�·ݵIJ���Ϊ![]() ��.
��.
����һ ��һ�·�������![]() ����ͧΪ
����ͧΪ![]() �����·�������
�����·�������![]() ����ͧΪ
����ͧΪ![]()
���ι�˾��ó�������һ�����·�������������ͧ�����п��ܽ����![]()
![]()
![]()
![]()
![]()
![]() �����֣�
�����֣�
����![]() ����ͧȫΪ���·������Ľ����
����ͧȫΪ���·������Ľ����![]() ��3�֣�
��3�֣�
����������ͧȫ��Ϊ���·������ĸ���Ϊ![]()
����������ͧ������һ��Ϊһ�·������ĸ���Ϊ![]() ��
��
�������ι�˾����ͧ���ٻصĸ���Ϊ��![]() .
.
���� ��һ�·�������![]() ����ͧΪ
����ͧΪ![]() ���·�������
���·�������![]() ����ͧΪ
����ͧΪ![]()
���ι�˾��ó�������һ�����·�������������ͧ�����п��ܽ����![]()
![]() ��10�֣����У�������ͧ������һ��Ϊһ�·������Ľ����
��10�֣����У�������ͧ������һ��Ϊһ�·������Ľ����![]() ��7�֣�
��7�֣�
����������ͧ������һ��Ϊһ�·������ĸ���Ϊ![]() ��
��
�������ι�˾����ͧ���ٻصĸ���Ϊ![]() .
.


 ���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У���
�У���![]() �ĶԱ߷ֱ�Ϊ
�ĶԱ߷ֱ�Ϊ![]() ����
����![]() �ɵȲ�����
�ɵȲ�����
��1����![]() ����
����![]() �����
�����
��2����![]() �ɵȱ����У����ж�
�ɵȱ����У����ж�![]() ����״
����״
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��װ���оٰ���һ���н���������˿�����ÿ����600Ԫ����600Ԫ�������ɳ齱һ�Σ��齱���������֣��˿�ֻ��ѡ�����е�һ�֣� ����һ����װ��10����״����С��ȫ��ͬ��С�����к���3��������7�����ij齱���У�һ���Գ��3��С�����н�����Ϊ��������3�����������ⵥ�Żݣ�������2���������6�ۣ�������1���������7�ۣ���û�������������ۣ�
����������װ��10����״����С��ȫ��ͬ��С�����к���3��������7�����ij齱���У��зŻص���ȡ������3�Σ�ÿ����1����������200Ԫ��
��1���������˿;��ֱ�������600Ԫ���Ҿ�ѡ��齱����һ��������λ�˿;������ⵥ�Żݵĸ��ʣ�
��2����ij�˿�����ǡ����1000Ԫ����ù˿�ѡ�����ֳ齱���������ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
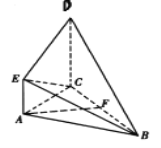
����Ŀ����ͼ��ʾ,ֱ������ACDE�����ֱ��������ABC����ƽ�滥�ഹֱ,FΪBC���е�,![]() ,
, ![]() ,
,![]() .
.
(1)��֤:ƽ��![]() ƽ��
ƽ��![]() ;
;
(2)��֤:![]() ƽ��
ƽ��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�� ![]() ʱ������
ʱ������ ![]() ��ͼ����
��ͼ���� ![]() ��ͼ������ֻ��һ�����㣬����ʵ��
��ͼ������ֻ��һ�����㣬����ʵ�� ![]() ��ȡֵ��Χ�� �� ��
��ȡֵ��Χ�� �� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���������˾ÿ��ƻ����������������ɡ����������߹� ![]() ��������һ��������
��������һ�������� ![]() ���ӣ�����һ�������
���ӣ�����һ������� ![]() ���ӣ�����һ��ɡ����
���ӣ�����һ��ɡ���� ![]() ���ӣ���֪������ʱ�䲻����
���ӣ���֪������ʱ�䲻���� ![]() Сʱ��������һ�������ɻ�����
Сʱ��������һ�������ɻ����� ![]() Ԫ������һ������ɻ�����
Ԫ������һ������ɻ����� ![]() Ԫ������һ��ɡ���ɻ�����
Ԫ������һ��ɡ���ɻ����� ![]() Ԫ.
Ԫ.
��1����ÿ���������������� ![]() ���������
��������� ![]() ��ʾÿ�������
��ʾÿ������� ![]() ��Ԫ����
��Ԫ����
��2����ô���������������ʹÿ������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ�����������ABCD��A1B1C1D1����Խ��� ![]() ����ƽ�����ƽ��C1BD��ƽ�����ƽ��ADD1A1=AS�����A1AS������ֵΪ�� ��
����ƽ�����ƽ��C1BD��ƽ�����ƽ��ADD1A1=AS�����A1AS������ֵΪ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʯͷ���������������ֳơ��¶��ǡ�����һ����������IJ�ȭ��Ϸ����Դ���й���Ȼ���ձ������ʵȵأ�������ŷó�IJ��Ϸ�չ����������ŷ�ޣ����˽����������磮����Ϸ�����ǣ���ȭ֮ǰ˫���뺰���Ȼ���ڻ�������ʱͬʱ��ȭ���ս���ȭͷ������ʯͷ����ʳָ����ָ�������������������ָ�쿪��������������ʯͷ��ʤ������������������ʤ������������������ʤ����ʯͷ������������ȭ��ͬ����Ϊ�;֣�Сǧ�ʹ�����λͬѧ���С������ʤ�ơ��ġ�ʯͷ��������������Ϸ��������Сǧ�ʹ�����������ľ�Сǧʤ���ĸ����ǣ� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��һ��1�����һ����ѧ���Գɼ��ľ�Ҷͼ��Ƶ�ʷֲ�ֱ��ͼ���ܵ���ͬ�̶ȵ��ƻ������ɼ�������ͼ���ҽ�ȫ��![]() �˵ijɼ���Ϊ
�˵ijɼ���Ϊ![]() ���ұߵij������к����
���ұߵij������к����![]() .�ݴ˽���������⣺
.�ݴ˽���������⣺
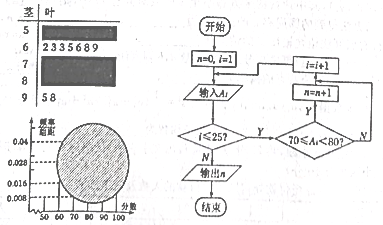
ע��ͼ��![]() ��ʾ���ǡ���
��ʾ���ǡ���![]() ��ʾ����
��ʾ����
��1����Ҷͼ����������![]() ��
��![]() ��
��![]() ������ε�Ƶ����
������ε�Ƶ����
��2������Ƶ�ʷֲ�ֱ��ͼ���Ƹð����ѧ���Գɼ�����������λ���ֱ��Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com