解:(1)当n=1时,
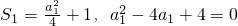
,解得a
1=2,
当n≥2时,
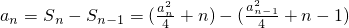
,整理得(a
n+a
n-1-2)(a
n-a
n-1-2)=0,
所以a
n-a
n-1=2,或a
n+a
n-1=2(不合题意,舍去,否则a
2n=0与已知矛盾),
∴数列{a
n}是等差数列,且公差为2,首项a
1=2,从而a
n=2n.(5分)
(2)数列{a
n}依次按1项,2项,3项循环地分为(2),(4,6),(8,10,12),(14),(16,18),(20,22,24),,每一次循环记为一组.由于每一个循环含有3个括号,故b
2009是第670组中第2个括号内各数之和.
由分组规律知,b
3,b
6,b
8,,b
2010,组成一个首项为b
3=8+10+12=30,公差为d=36的等差数列.所以b
2010=30+(670-1)×36=24114.(10分)
(3)当n是m的整数倍时,求b
n的值.
数列{a
n}依次按1项、2项、3项,,m项循环地分为(2),(4,6),(8,10,12),,(m
2-m+2,m
2-m+4,m
2-m+6,,m
2+m);(m
2+m+2)(m
2+m+4,m
2+m+6),,(2m
2+2,2m
2+4,,2m
2+2m),(2m
2+2m+2),
第m组,第2m组,,第km(k∈N
*)组的第1个数,第2个数,,第m个数分别组成一个等差数列,其首项分别为m
2-m+2,m
2-m+4,m
2-m+6,,m
2+m公差均为m(m+1)
则第m组、第2m组,,第km组,的各数之和也组成一个等差数列,其公差为m
2(m+1)
第m组的m个数之和为
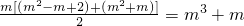
∴当n=km时,b
n=b
km=m
3+m+(k-1)m
2(m+1).(16分)
分析:(1)由:
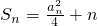
,可用a
n与S
n的关系求解;
(2)先由数列{a
n}将(a
1),(a
2,a
3),(a
4,a
5,a
6),(a
7),(a
8,a
9),(a
10,a
11,a
12),转化为(2),(4,6),(8,10,12),(14),(16,18),(20,22,24),按照每一次循环记为一组.由于每一个循环含有3个括号的规律抽象出b
3,b
6,b
8,,b
2010,组成一个首项为b
3,公差为36的等差数列.
(3)由“提出同(2)类似的问题((2)应当作为特例)”即研究:当n是m的整数倍时,求b
n.按照(2)的思路解决.
点评:本题考查通项和前n项和之间的关系,由数列构造新数列和转化数列的能力.

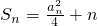 ,an>0.
,an>0.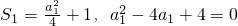 ,解得a1=2,
,解得a1=2,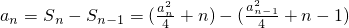 ,整理得(an+an-1-2)(an-an-1-2)=0,
,整理得(an+an-1-2)(an-an-1-2)=0,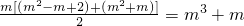
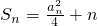 ,可用an与Sn的关系求解;
,可用an与Sn的关系求解;

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案