
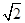 EF.
EF.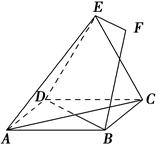
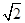 BO=AB,又因为AB=
BO=AB,又因为AB=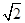 EF,∴BO=EF,又因为EF∥BD,∴EFBO是平行四边形,∴BF∥EO,又∵BF?平面ACE,EO?平面ACE,∴BF∥平面ACE.列线面平行判定定理的条件必须要全面. (2)证明线线垂直,一般利用线面垂直进行转化.条件为面面垂直,所以先由面面垂直性质定理转化为线面垂直:正方形ABCD中,AC⊥BD,又因为正方形ABCD和三角形ACE所在的平面互相垂直,BD?平面ABCD,平面ABCD∩平面ACE=AC,∴BD⊥平面ACE,∵EO?平面ACE,∴BD⊥EO,∵EO∥BF,∴BF⊥BD.
EF,∴BO=EF,又因为EF∥BD,∴EFBO是平行四边形,∴BF∥EO,又∵BF?平面ACE,EO?平面ACE,∴BF∥平面ACE.列线面平行判定定理的条件必须要全面. (2)证明线线垂直,一般利用线面垂直进行转化.条件为面面垂直,所以先由面面垂直性质定理转化为线面垂直:正方形ABCD中,AC⊥BD,又因为正方形ABCD和三角形ACE所在的平面互相垂直,BD?平面ABCD,平面ABCD∩平面ACE=AC,∴BD⊥平面ACE,∵EO?平面ACE,∴BD⊥EO,∵EO∥BF,∴BF⊥BD.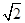 BO=AB,又因为AB=
BO=AB,又因为AB=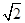 EF,
EF,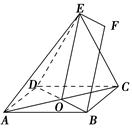


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源:不详 题型:解答题
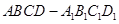 中,
中,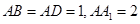 ,G是
,G是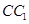 上的动点。
上的动点。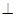
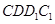 ;
;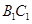 与平面ADG的位置关系,并给出证明;
与平面ADG的位置关系,并给出证明;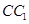 的中点,求二面角G-AD-C的大小;
的中点,求二面角G-AD-C的大小;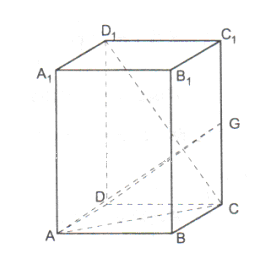
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.充分不必要条件 |
| B.必要不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
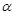 、
、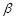 为两个不同的平面,下列命题中正确的是( )
为两个不同的平面,下列命题中正确的是( ) A.若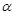 ∥ ∥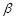 ,m∥ ,m∥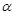 ,则m∥ ,则m∥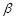 |
B.若m⊥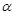 ,m⊥ ,m⊥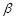 ,则 ,则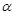 ∥ ∥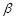 |
C.若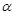 ⊥ ⊥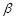 ,m⊥ ,m⊥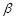 ,则m⊥ ,则m⊥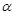 |
D.若m∥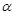 ,m⊥n,则n⊥ ,m⊥n,则n⊥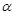 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
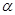 与平面
与平面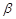 平行的条件可以是( )
平行的条件可以是( ) A.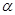 内有无穷多条直线与 内有无穷多条直线与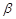 平行 平行 | B.直线a//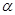 ,a// ,a//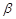 |
C.直线a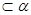 ,直线b ,直线b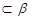 ,且a// ,且a//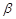 ,b// ,b//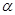 | D.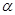 内的任何直线都与 内的任何直线都与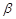 平行 平行 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
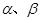 ,且
,且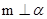 ,
,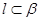 .给出下列命题:
.给出下列命题: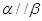 ,则
,则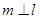 ;
;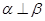 ,则
,则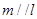 ;
;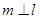 ,则
,则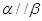 ;
;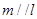 ,则
,则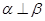 ,
,| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com