
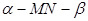 的大小为
的大小为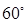 ,菱形
,菱形 在面
在面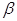 内,
内,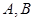 两点在棱
两点在棱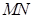 上,
上,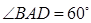 ,
,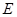 是
是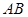 的中点,
的中点,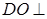 面
面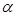 ,垂足为
,垂足为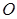 .
.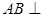 平面
平面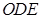 ;
;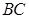 与
与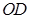 所成角的余弦值.
所成角的余弦值.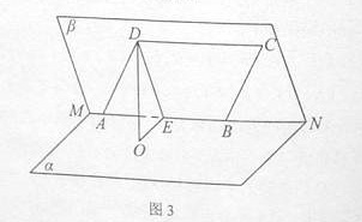
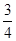
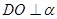 ,利用线面垂直的性质可得
,利用线面垂直的性质可得
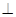
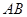 ,已知角
,已知角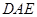 和
和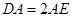 ,利用余弦定理即可说明
,利用余弦定理即可说明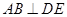 ,即
,即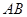 垂直于面
垂直于面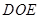 内两条相交的直线,根据线面垂直的判断即可得到直线
内两条相交的直线,根据线面垂直的判断即可得到直线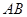 垂直于面
垂直于面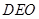 .
.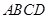 为菱形可得
为菱形可得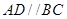 ,则
,则 与
与 所成角与角
所成角与角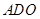 大小相等,即求
大小相等,即求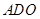 角的余弦值即可,利用菱形
角的余弦值即可,利用菱形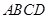 所有边相等和一个角为
所有边相等和一个角为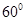 即可求的
即可求的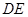 的长度,根据(1)可得
的长度,根据(1)可得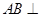 面
面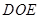 ,即角
,即角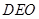 为二面角
为二面角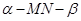 的平面角为
的平面角为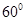 ,结合
,结合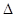
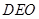 为直角三角形与
为直角三角形与 的长度,即可求的
的长度,即可求的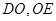 长度,再直角
长度,再直角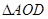 中,
中,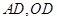 已知,利用直角三角形中余弦的定义即可求的角
已知,利用直角三角形中余弦的定义即可求的角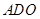 的余弦值,进而得到异面直线夹角的余弦值.
的余弦值,进而得到异面直线夹角的余弦值.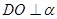 ,
,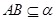 ,所以
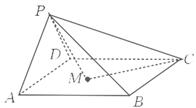
,所以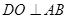 ,连接
,连接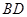 ,由题可知
,由题可知 是正三角形,又
是正三角形,又 是
是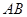 的中点,所以
的中点,所以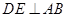 ,而
,而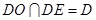 ,故
,故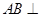 平面
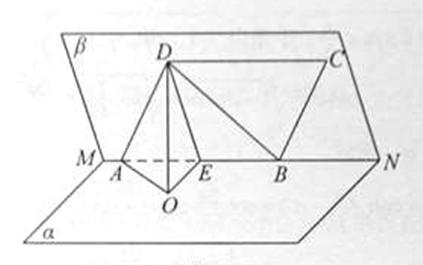
平面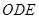 .
.
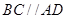 ,所以
,所以 与
与 所成的角等于
所成的角等于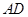 与
与 所成的角,即
所成的角,即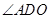 是
是 与
与 所成的角,由(1)可知,
所成的角,由(1)可知,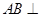 平面
平面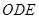 ,所以
,所以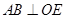 ,又
,又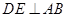 ,于是
,于是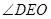 是二面角
是二面角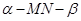 的平面角,从而
的平面角,从而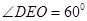 ,不妨设
,不妨设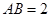 ,则
,则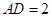 ,易知
,易知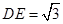 ,在
,在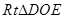 中,
中,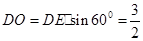 ,连接
,连接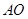 ,在
,在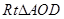 中,
中, ,所以异面直线
,所以异面直线 与
与 所成角的余弦值为
所成角的余弦值为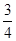 .
.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源:不详 题型:解答题
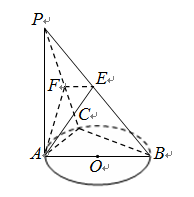
 ,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1.
,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1.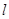 ,求证:
,求证: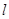 ∥平面BCDE;
∥平面BCDE;
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.α⊥β,且m?α | B.m∥n,且n⊥β |
| C.α⊥β,且m∥α | D.m⊥n,且n∥β |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
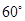 ,则称这对异面直线为“黄金异面直线对”,在连接正方体各顶点的所有直线中,“黄金异面直线对”共有( )
,则称这对异面直线为“黄金异面直线对”,在连接正方体各顶点的所有直线中,“黄金异面直线对”共有( )| A.12对 | B.18对 | C.24对 | D.30对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com