
| A. | n=4时该命题不成立 | |
| B. | n=6时该命题不成立 | |
| C. | n为大于5的某个自然数时该命题成立 | |
| D. | 以上答案均不对 |
分析 由归纳法的性质,我们由P(n)对n=k成立,则它对n=k+1也成立,由此类推,对n>k的任意整数均成立,结合逆否命题同真同假的原理,当P(n)对n=k不成立时,则它对n=k-1也不成立,由此类推,对n<k的任意正整数均不成立,由此不难得到答案.
解答 解:由题意可知,
P(n)对n=4不成立(否则n=5也成立).
同理可推得P(n)对n=3,n=2,n=1也不成立.
故选A.
点评 当P(n)对n=k成立,则它对n=k+1也成立,由此类推,对n>k的任意整数均成立;结合逆否命题同真同假的原理,当P(n)对n=k不成立时,则它对n=k-1也不成立,由此类推,对n<k的任意正整数均不成立.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
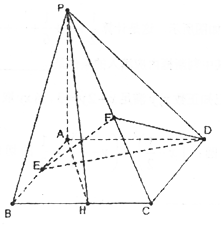 如图,四棱锥P-ABCD的底面为正方形,侧面PAD⊥底面ABCD,PA⊥AD,E,F,H分别为AB,PC,BC的中点.
如图,四棱锥P-ABCD的底面为正方形,侧面PAD⊥底面ABCD,PA⊥AD,E,F,H分别为AB,PC,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
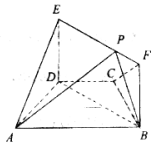 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=2-x | B. | f(x)=x2 | C. | f(x)=3-x | D. | f(x)=cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com