
分析 (1)先根据导数的几何意义求出f(x)在x=0处的切线方程,再与g(x)联立构成方程组,消元,根据判别式即可求出a的值.
(2)表示出M,N的坐标,求出h(x)的表达式,再根据导数和函数的极值的关系即可求出a的值.
解答 解(1):f'(x)=ex,
∴在x=0即切点为(0,1)处的切线斜率k=f'(0)=1,
即切线为y=x+1,
∴联立$\left\{{\begin{array}{l}{y=x+1}\\{y=-{x^2}+ax-a}\end{array}}\right.$,得x2+(1-a)x+1+a=0,
由相切得△=(1-a)2-4(1+a)=0,
解得$a=3±2\sqrt{3}$
(2)M(x,ex),N(x,-x2+ax-a),
∴h(x)=x2-ex(x2-ax+a),
∴h'(x)=2x-ex[x2+(2-a)x]=-x[ex(x+2-a)-2],
由h(x)取得极值,则x=0或ex(x+2-a)-2=0,
∴$a=x+2-\frac{2}{e^x}$,令$F(x)=x+2-\frac{2}{e^x}$,该函数在R上单调递增,
∴存在唯一的x0∈R,使得F(x0)=a,
①若x0>0,则
| x | (-∞,0) | 0 | (0,x0) | x0 | (x0,+∞) |
| h'(x) | - | 0 | + | 0 | - |
| h(x) | 递减 | 极小 | 递增 | 极大 | 递减 |
| x | (-∞,0) | (0,+∞) |
| h'(x) | - | - |
| h(x) | 递减 | 递减 |
| x | (-∞,x0) | x0 | (x0,0) | 0 | (0,+∞) |
| h'(x) | - | 0 | + | 0 | - |
| h(x) | 递减 | 极小值 | 递增 | 极大值 | 递减 |
点评 本题考查利用导数研究过曲线上某点处的切线方程,考查了利用导数研究函数的单调性和极值,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}({2}^{n}-1)$ | B. | $\frac{5}{18}({3}^{n}-1)$ | C. | $5•{2}^{n-1}-\frac{5}{4}$ | D. | $5•{2}^{n-2}-\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
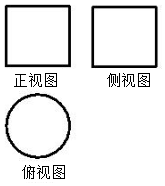
| A. | 6π | B. | $8\sqrt{2}$π | C. | $4+4\sqrt{2}$π | D. | $8+4\sqrt{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 时间代号t | 1 | 2 | 3 | 4 | 5 |
| 外来资金y(百亿元) | 5 | 6 | 7 | 8 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=|x|和g(x)=$\sqrt{{x}^{2}}$ | B. | f(x)=$\sqrt{{x}^{2}}$和 g(x)=($\sqrt{x}$)2 | ||
| C. | f(x)=$\frac{{x}^{2}-1}{x-1}$和g(x)=x+1 | D. | f(x)=x-1与g(x)=$\frac{{x}^{2}}{x}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com