Question

1．如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，∠BCD=135°，侧面PAB⊥底面ABCD，∠BAP=90°，AB=AC=PA=2，E，F分别为BC，AD的中点，点M在线段PD上．
（Ⅰ）求证：EF⊥平面PAC； 
（Ⅱ）若M为PD的中点，求证：ME∥平面PAB；
（Ⅲ）如果直线ME与平面PBC所成的角和直线ME与平面ABCD所成的角相等，求$\frac{PM}{PD}$的值．

Answer 1

分析 （Ⅰ）证明AB⊥AC．EF⊥AC．推出PA⊥底面ABCD，即可说明PA⊥EF，然后证明EF⊥平面PAC．
（Ⅱ）证明MF∥PA，然后证明MF∥平面PAB，EF∥平面PAB．即可阿门平面MEF∥平面PAB，从而证明ME∥平面PAB．
（Ⅲ）以AB，AC，AP分别为x轴、y轴和z轴，如上图建立空间直角坐标系，求出相关点的坐标，平面ABCD的法向量，平面PBC的法向量，利用直线ME与平面PBC所成的角和此直线与平面ABCD所成的角相等，列出方程求解即可

解答 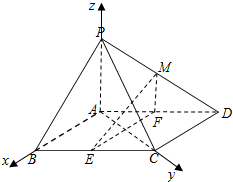（本小题满分14分）
（Ⅰ）证明：在平行四边形ABCD中，因为AB=AC，∠BCD=135°，∠ABC=45°．
所以AB⊥AC．
由E，F分别为BC，AD的中点，得EF∥AB，
所以EF⊥AC．…（1分）
因为侧面PAB⊥底面ABCD，且∠BAP=90°，
所以PA⊥底面ABCD．…（2分）
又因为EF?底面ABCD，
所以PA⊥EF．…（3分）
又因为PA∩AC=A，PA?平面PAC，AC?平面PAC，
所以EF⊥平面PAC．…（4分）
（Ⅱ）证明：因为M为PD的中点，F分别为AD的中点，
所以MF∥PA，
又因为MF?平面PAB，PA?平面PAB，
所以MF∥平面PAB．…（5分）
同理，得EF∥平面PAB．
又因为MF∩EF=F，MF?平面MEF，EF?平面MEF，
所以平面MEF∥平面PAB．…（7分）
又因为ME?平面MEF，
所以ME∥平面PAB．…（9分）
（Ⅲ）解：因为PA⊥底面ABCD，AB⊥AC，所以AP，AB，AC两两垂直，故以AB，AC，AP
分别为x轴、y轴和z轴，如上图建立空间直角坐标系，
则A（0，0，0），B（2，0，0），C（0，2，0），P（0，0，2），D（-2，2，0），E（1，1，0），
所以$\overrightarrow{PB}=（2，0，-2）$，$\overrightarrow{PD}=（-2，2，-2）$，$\overrightarrow{BC}=（-2，2，0）$，…（10分）
设$\frac{PM}{PD}={λ_{\;}}（λ∈[0，1]）$，则$\overrightarrow{PM}=（-2λ，2λ，-2λ）$，
所以M（-2λ，2λ，2-2λ），$\overrightarrow{ME}=（1+2λ，1-2λ，2λ-2）$，
易得平面ABCD的法向量$\overrightarrow{m}$=（0，0，1）．…（11分）
设平面PBC的法向量为$\overrightarrow{n}$=（x，y，z），
由$\overrightarrow{n}•\overrightarrow{BC}=0$，$\overrightarrow{n}•\overrightarrow{PB}=0$，得$\left\{\begin{array}{l}-2x+2y=0\\ 2x-2z=0\end{array}\right.$
令x=1，得$\overrightarrow{n}$=（1，1，1）．…（12分）
因为直线ME与平面PBC所成的角和此直线与平面ABCD所成的角相等，
所以$|cos＜\overrightarrow{ME}，\overrightarrow{m}＞|=|cos＜\overrightarrow{ME}，\overrightarrow{n}＞|$，即$\frac{|\overrightarrow{ME}•\overrightarrow{m}|}{|\overrightarrow{ME}|•|\overrightarrow{m}|}=\frac{|\overrightarrow{ME}•\overrightarrow{n}|}{|\overrightarrow{ME}|•|\overrightarrow{n}|}$，…（13分）
所以 $|2λ-2|=|\frac{2λ}{{\sqrt{3}}}|$，
解得$λ=\frac{{3-\sqrt{3}}}{2}$，或$λ=\frac{{3+\sqrt{3}}}{2}$（舍）．…（14分）

点评 本题考查直线与平面所成角的求法，直线与平面平行的判定定理以及性质定理的应用，平面与平面平行的判定定理的应用，考查转化思想以及空间想象能力逻辑推理能力的应用．