[题目]在极坐标系中.设直线过点A( . ).B(3. ).且直线与曲线C:ρ=2rsinθ有且只有一个公共点.求实数r的值．题目和参考答案——青夏教育精英家教网—

【题目】在极坐标系中，设直线过点A（，），B（3，），且直线与曲线C：ρ=2rsinθ（r＞0）有且只有一个公共点，求实数r的值．

【答案】解：点A（，），B（3，），分别化为直角坐标A ，B ，即A ，B（0，3）．
∴直线AB的方程为：y= x+3，化为：y= +3．
直线与曲线C：ρ=2rsinθ（r＞0）化为：ρ2=2rρsinθ，可得直角坐标方程：x2+y2=2ry，配方为：x2+（y﹣r）2=r2 ，可得圆心C（0，r），半径r．
∵直线与曲线C：ρ=2rsinθ（r＞0）有且只有一个公共点，
∴直线与圆C相切，∴ =r，解得r=1
【解析】把极坐标及其极坐标方程化为直角坐标方程，利用直线与圆相切的充要条件即可得出．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】函数f(x)的导函数为f′(x)，对任意的x∈R，都有2f′(x)>f(x)成立，则(　　)

A. 3f(2ln 2)>2f(2ln 3)

B. 3f(2ln 2)<2f(2ln 3)

C. 3f(2ln 2)＝2f(2ln 3)

D. 3f(2ln 2)与2f(2ln 3)的大小不确定

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设函数f（x）=x3﹣12x+b，则下列结论正确的是（）
A.函数f（x）在（﹣∞，﹣1）上单调递增
B.函数f（x）在（﹣∞，﹣1）上单调递减
C.若b=﹣6，则函数f（x）的图象在点（﹣2，f（﹣2））处的切线方程为y=10
D.若b=0，则函数f（x）的图象与直线y=10只有一个公共点

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在平面直角坐标系xOy中，D是到原点的距离不大于1的点构成的区域，E是满足不等式组的点（x，y）构成的区域，向D中随机投一点，则所投的点落在E中的概率是．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：

单价x(元)	9	9.2	9.4	9.6	9.8	10
销量y(件)	100	94	93	90	85	78

(1)求回归直线方程求回归直线方程.

(2)预计在今后的销售中，销量与单价仍然服从(1)中的关系，且该产品的成本是5元/件，为使工厂获得最大利润，该产品的单价应定为多少元？(利润＝销售收入－成本)

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，江的两岸可近似的看成两平行的直线，江岸的一侧有A，B两个蔬菜基地，江的另一侧点C处有一个超市．已知A、B、C中任意两点间的距离为20千米．超市欲在AB之间建一个运输中转站D，A，B两处的蔬菜运抵D处后，再统一经过货轮运抵C处．由于A，B两处蔬菜的差异，这两处的运输费用也不同．如果从A处出发的运输费为每千米2元，从B处出发的运输费为每千米1元，货轮的运输费为每千米3元．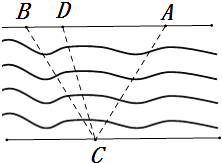

（1）设∠ADC=α，试将运输总费用S（单位：元）表示为α的函数S（α），并写出自变量的取值范围；
（2）问中转站D建在何处时，运输总费用S最小？并求出最小值．