
分析 (1)根据函数零点定理,令f(x)=0,即可求出函数的零点,再写出数列的通项公式即可,
(2)分n≤4或n≥4两种情况根据等差数列的求和公式计算即可,
(3)求出bn=n,当n>1时,再利用$\frac{1}{{b}_{1}{b}_{2}…{b}_{n}}$=$\frac{1}{1×2×3×…×n}$<$\frac{1}{n(n-1)}$=$\frac{1}{n}$-$\frac{1}{n-1}$,再利用放缩即可证明.
解答 解:(1)令f(x)=sinx=0
解得x=kπ,取k∈N,且k≥-3,
则an=nπ-4π,n∈N*.
(2)由(1)知数列的{an}的首项为-3π,公差为π,
{|an|}的前n项和Sn;
当n≤4时,Sn=-$\frac{n({a}_{1}+{a}_{n})}{2}$=-$\frac{n(-3π+nπ-4π)}{2}$=$\frac{n(7π-nπ)}{2}$,
当n>4时,数列{|an|}的前n项和Sn=-a1-a2-a3-a4+a5+…+an=a1+a2+a3+a4+a5+…+an-2(a1+a2+a3+a4)=$\frac{n(-3π+nπ-4π)}{2}$-12π=$\frac{n(nπ-7π)}{2}$+12π
∴Sn=$\left\{\begin{array}{l}{\frac{n(7π-nπ)}{2},n≤4}\\{\frac{n(nπ-7π)}{2}+12π,n>4}\end{array}\right.$,
(3)bn=$\frac{{a}_{n}}{π}$+4=n-4+4=n,
∴b1b2b3…bn=1×2×3×…×n,
∴$\frac{1}{{b}_{1}}$+$\frac{1}{{{b}_{1}b}_{2}}$+$\frac{1}{{{{b}_{1}b}_{2}b}_{3}}$+$\frac{1}{{{{{b}_{1}b}_{2}b}_{3}b}_{4}}$+…+$\frac{1}{{{{b}_{1}b}_{2}b}_{3}••{•b}_{2017}}$,
=$\frac{1}{1}$+$\frac{1}{1×2}$+$\frac{1}{1×2×3}$+$\frac{1}{1×2×3×4}$+…+$\frac{1}{1×2×3×…×2017}$,
<1+$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2016×2017}$,
=1+1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2006}$-$\frac{1}{2007}$=2-$\frac{1}{2007}$<2
点评 本题考查了函数零点定理和数列的通项公式和等差数列的前n项和公式以及放缩法和裂项求和,属于中档题


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
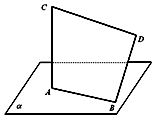 如图,线段AB在平面α内,线段BD⊥AB,线段AC⊥α,且AB=$\frac{7}{2}$,AC=BD=12,CD=$\frac{25}{2}$,求线段BD与平面α所成的角.
如图,线段AB在平面α内,线段BD⊥AB,线段AC⊥α,且AB=$\frac{7}{2}$,AC=BD=12,CD=$\frac{25}{2}$,求线段BD与平面α所成的角.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.6826 | B. | 0.9544 | C. | 0.2718 | D. | 0.1359 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18个 | B. | 16个 | C. | 14个 | D. | 12个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com