
【题目】下列每组函数是同一函数的是( )
A.f(x)=x0与f(x)=1
B.f(x)= ![]() ﹣1与f(x)=|x|﹣1
﹣1与f(x)=|x|﹣1
C.f(x)= ![]() 与f(x)=x﹣2
与f(x)=x﹣2
D.f(x)= ![]() 与f(x)=
与f(x)= ![]()
【答案】B
【解析】解:对于A:f(x)=x0的定义域为{x|x≠0},而f(x)=1的定义域为R,定义域不同,∴不是同一函数;对于B:f(x)= ![]() ﹣1=|x|﹣1,的定义域为R,而f(x)=|x|﹣1的定义域为R,它们定义域相同,对应关系也相同,∴是同一函数;
﹣1=|x|﹣1,的定义域为R,而f(x)=|x|﹣1的定义域为R,它们定义域相同,对应关系也相同,∴是同一函数;
对于C:f(x)= ![]() 的定义域为{x|x≠﹣2},而与f(x)=x﹣2的定义域为R,定义域不同,∴不是同一函数;
的定义域为{x|x≠﹣2},而与f(x)=x﹣2的定义域为R,定义域不同,∴不是同一函数;
对于D:f(x)= ![]() 的定义域为{x|x≥2或x≤1},而f(x)=
的定义域为{x|x≥2或x≤1},而f(x)= ![]() 的定义域为{x|x≥2},定义域不同,∴不是同一函数;
的定义域为{x|x≥2},定义域不同,∴不是同一函数;
故选B.
【考点精析】解答此题的关键在于理解判断两个函数是否为同一函数的相关知识,掌握只有定义域和对应法则二者完全相同的函数才是同一函数.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,按其数学成绩(均为整数)分成六组![]() ,
, ![]() ,…,
,…, ![]() 后得到如下部分频率分布直方图,观察图中的信息,回答下列问题:
后得到如下部分频率分布直方图,观察图中的信息,回答下列问题:
(1)补全频率分布直方图;
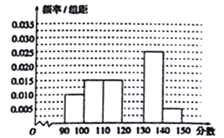
(2)估计本次考试的数学平均成绩(同一组中的数据用该组区间的中点值作代表);
(3)用分层抽样的方法在分数段为![]() 的学生成绩中抽取一个容量为6的样本,再从这6个样本中任取2人成绩,求至多有1人成绩在分数段
的学生成绩中抽取一个容量为6的样本,再从这6个样本中任取2人成绩,求至多有1人成绩在分数段![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx+c(a≠0)的图象过点(0,1)且与x轴有唯一的交点(﹣1,0). (Ⅰ)求f(x)的表达式;
(Ⅱ)在(Ⅰ)的条件下,设函数F(x)=f(x)﹣mx,若F(x)在区间[﹣2,2]上是单调函数,求实数m的取值范围;
(Ⅲ)设函数g(x)=f(x)﹣kx,x∈[﹣2,2],记此函数的最小值为h(k),求h(k)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,已知曲线![]() 的参数方程为
的参数方程为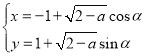 (
(![]() 为参数,
为参数,![]() ).
).
(Ⅰ)当![]() 时,若曲线
时,若曲线![]() 上存在
上存在![]() 两点关于点
两点关于点![]() 成中心对称,求直线
成中心对称,求直线![]() 的参数方程;
的参数方程;
(Ⅱ)在以原点为极点,![]() 轴正半轴为极轴的极坐标系中,极坐标方程为
轴正半轴为极轴的极坐标系中,极坐标方程为![]() 的直线
的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若
两点,若![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;
(2)若f(x)在区间[2a,a+1]上不单调,求a的取值范围
(3)若x∈[t,t+2],试求y=f(x)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左焦点为
的左焦点为![]() ,设
,设![]() 是椭圆
是椭圆![]() 的两个短轴端点,
的两个短轴端点,![]() 是椭圆
是椭圆![]() 的长轴左端点.
的长轴左端点.
(Ⅰ)当![]() 时,设点
时,设点![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,且直线
,且直线![]() 的斜率分别为
的斜率分别为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)当![]() 时,若经过
时,若经过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,O为坐标原点,求
两点,O为坐标原点,求![]() 与
与![]() 的面积之差的最大值.
的面积之差的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]()
(1)若不等式![]() 对
对![]() 恒成立,求
恒成立,求![]() 的值;
的值;
(2)若![]() 在
在![]() 内有两个极值点,求负数
内有两个极值点,求负数![]() 的取值范围;
的取值范围;
(3)已知 ,若对任意实数
,若对任意实数![]() ,总存在实数
,总存在实数![]() ,使得
,使得![]() 成立,求正实数
成立,求正实数![]() 的取值集合.
的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应边分别是a,b,c,c=2,sin2A+sin2B﹣sin2C=sinAsinB.
(1)若sinC+sin(B﹣A)=2sin2A,求△ABC面积;
(2)求AB边上的中线长的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家父母记录了女儿玥玥的年龄(岁)和身高(单位cm)的数据如下:
年龄x | 6 | 7 | 8 | 9 |
身高y | 118 | 126 | 136 | 144 |
(1)试求y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]()
(2)试预测玥玥10岁时的身高.(其中, ![]() =
= 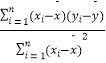 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com