
【题目】某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选出了三个科目作为选考科目.若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.某学校为了了解高一年级200名学生选考科目的意向,随机选取20名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有5人 | 5 | 5 | 2 | 1 | 2 | 0 |
选考方案待确定的有7人 | 6 | 4 | 3 | 2 | 4 | 2 | |
女生 | 选考方案确定的有6人 | 3 | 5 | 2 | 3 | 3 | 2 |
选考方案待确定的有2人 | 1 | 2 | 1 | 0 | 1 | 1 |
(1)在选考方案确定的男生中,同时选考物理、化学、生物的人数有多少?
(2)从选考方案确定的男生中任选2名,试求出这2名学生选考科目完全相同的概率.
【答案】(1)2人;(2)![]()
【解析】
(1)由表格可直接发现选考方案确定的男生中同时选择“物理、化学和生物”的人数.
(2)已确定选考科目的男生共5人.其中有2人选择“物理、化学和生物”,记为![]() ,
,![]() ;有1人选择“物理、化学和历史”,记为
;有1人选择“物理、化学和历史”,记为![]() ;有2人选择“物理、化学和地理”,记为
;有2人选择“物理、化学和地理”,记为![]() ,
,![]() ,由此利用列举法能求出任取2名男生,这2名学生选考科目完全相同的概率.
,由此利用列举法能求出任取2名男生,这2名学生选考科目完全相同的概率.
(1)选考方案确定的男生中,同时选择“物理、化学和生物”的人数是2人.
(2)由数据可知,已确定选考科目的男生共5人.其中有2人选择“物理、化学和生物”,记为![]() ,
,![]() ;有1人选择“物理、化学和历史”,记为
;有1人选择“物理、化学和历史”,记为![]() ;有2人选择“物理、化学和地理”,记为
;有2人选择“物理、化学和地理”,记为![]() ,
,![]() .
.
从已确定选考科目的男生中任选2人,有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共10种选法.
,共10种选法.
两位学生选考科目完全相同的选法种数有![]() ,
,![]() ,共2种选法.
,共2种选法.
设事件![]() :从已确定选考科目的男生中任选出2人,这两位学生选考科目完全相同.
:从已确定选考科目的男生中任选出2人,这两位学生选考科目完全相同.
则![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且椭圆C过点
,且椭圆C过点![]() .
.
(1)求椭圆C的标准方程;
(2)过椭圆C的右焦点的直线l与椭圆C交于A、B两点,且与圆:![]() 交于E、F两点,求
交于E、F两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于直线
中,对于直线![]() 和点
和点![]() 、
、![]() ,记
,记![]() ,若
,若![]() ,则称点
,则称点![]() ,
,![]() 被直线l分隔,若曲线C与直线l没有公共点,且曲线C上存在点
被直线l分隔,若曲线C与直线l没有公共点,且曲线C上存在点![]() ,
,![]() 被直线l分隔,则称直线l为曲线C的一条分隔线.
被直线l分隔,则称直线l为曲线C的一条分隔线.
(1)求证:点![]() 、
、![]() 被直线
被直线![]() 分隔;
分隔;
(2)若直线![]() 是曲线
是曲线![]() 的分隔线,求实数
的分隔线,求实数![]() 的取值范围;
的取值范围;
(3)动点M到点![]() 的距离与到y轴的距离之积为1,设点M的轨迹为E,求E的方程,并证明y轴为曲线E的分隔线.
的距离与到y轴的距离之积为1,设点M的轨迹为E,求E的方程,并证明y轴为曲线E的分隔线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,过点P(0,1)且互相垂直的两条直线分別与圆O:![]() 交于点A,B,与圆M:(x﹣2)2+(y﹣1)2=1交于点C,D.
交于点A,B,与圆M:(x﹣2)2+(y﹣1)2=1交于点C,D.
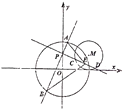
(1)若AB=![]() ,求CD的长;
,求CD的长;
(2)若CD中点为E,求△ABE面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到直线
到直线![]() 的距离相等.
的距离相等.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 且斜率为1的直线与曲线
且斜率为1的直线与曲线![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() ,
,![]() 为坐标原点,求
为坐标原点,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com