
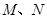 为圆
为圆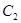 与
与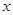 轴的两个交点.
轴的两个交点.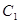 的方程;
的方程;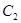 在抛物线上运动时,试判断
在抛物线上运动时,试判断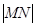 是否为一定值?请证明你的结论;
是否为一定值?请证明你的结论;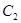 在抛物线上运动时,记
在抛物线上运动时,记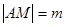 ,
,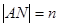 ,求
,求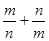 的最大值.
的最大值.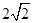
 ,又C1经过点P(2,2),即可求出抛物线的
,又C1经过点P(2,2),即可求出抛物线的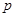 .即可得抛物线的方程.
.即可得抛物线的方程.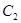 在抛物线上运动时,写出圆
在抛物线上运动时,写出圆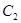 的方程,再令y=0即可求得圆的方程与x轴的两交点的坐标,计算两坐标的差即可得到结论.
的方程,再令y=0即可求得圆的方程与x轴的两交点的坐标,计算两坐标的差即可得到结论.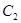 在抛物线上运动时,由(1)可得M,N的坐标(其中用圆心
在抛物线上运动时,由(1)可得M,N的坐标(其中用圆心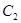 的坐标表示).根据两点的距离公式即可用圆心
的坐标表示).根据两点的距离公式即可用圆心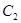 的坐标表示m,n的值,将
的坐标表示m,n的值,将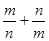 适当变形,再根据基本不等式即可求得
适当变形,再根据基本不等式即可求得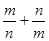 的最大值.
的最大值.
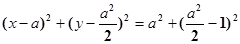 .
. ,
,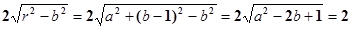 (定值)---7分
(定值)---7分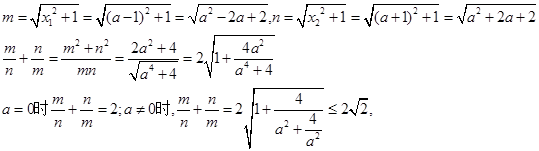



湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com