
如图所示,在四边形A-BCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A?BCD,则在三棱锥ABCD中,下列命题正确的是( ).

A.平面ABD⊥平面ABC
B.平面ADC⊥平面BDC
C.平面ABC⊥平面BDC
D.平面ADC⊥平面ABC
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练18练习卷(解析版) 题型:解答题
某商场为吸引顾客消费推出一项促销活动,促销规则如下:到该商场购物消费满100元就可转动如图所示的转盘一次,进行抽奖(转盘为十二等分的圆盘),满200元转两次,以此类推;在转动过程中,假定指针停在转盘的任一位置都是等可能的;若转盘的指针落在A区域,则顾客中一等奖,获得10元奖金;若转盘落在B区域或C区域,则顾客中二等奖,获得5元奖金;若转盘指针落在其他区域,则不中奖(若指针停到两区间的实线处,则重新转动).若顾客在一次消费中多次中奖,则对其奖励进行累加.已知顾客甲到该商场购物消费了268元,并按照规则参与了促销活动.
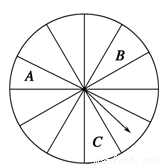
(1)求顾客甲中一等奖的概率;
(2)记X为顾客甲所得的奖金数,求X的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练15练习卷(解析版) 题型:选择题
已知椭圆E: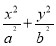 =1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A,B两点.若AB的中点坐标为(1,-1),则E的方程为( ).
=1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A,B两点.若AB的中点坐标为(1,-1),则E的方程为( ).
A. 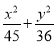 =1 B.
=1 B. 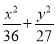 =1 C.
=1 C. 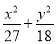 =1 D.
=1 D.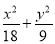 =1
=1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练13练习卷(解析版) 题型:填空题
已知ABCD-A1B1C1D1为正方体,①( +
+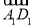 +
+ )2=3
)2=3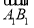 2;②
2;② ·(
·(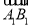 -
-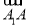 )=0;③向量
)=0;③向量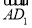 与向量
与向量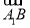 的夹角是60°;④正方体ABCD-A1B1C1D1的体积为|
的夹角是60°;④正方体ABCD-A1B1C1D1的体积为|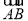 ·
·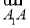 ·
·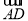 |.其中正确命题的序号是________.
|.其中正确命题的序号是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练12练习卷(解析版) 题型:解答题
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,M是PD的中点,AB=2,∠BAD=60°.

(1)求证:OM∥平面PAB;
(2)求证:平面PBD⊥平面PAC;
(3)当四棱锥P-ABCD的体积等于 时,求PB的长.
时,求PB的长.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练11练习卷(解析版) 题型:解答题
已知四棱锥P?ABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC,AD的中点.
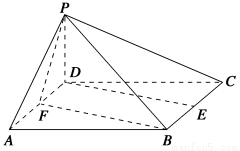
(1)求证:DE∥平面PFB;
(2)已知二面角P?BF?C的余弦值为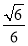 ,求四棱锥P?ABCD的体积.
,求四棱锥P?ABCD的体积.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练11练习卷(解析版) 题型:选择题
某四棱台的三视图如图所示,则该四棱台的体积是( ).
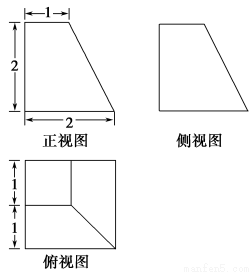
A.4 B. 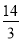 C.
C.  D.6
D.6
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷5练习卷(解析版) 题型:解答题
如图,在平面直角坐标系xOy中,椭圆C: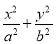 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为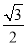 ,以坐标原点为圆心,椭圆C的短半轴长为半径的圆与直线x-y+2=0相切.
,以坐标原点为圆心,椭圆C的短半轴长为半径的圆与直线x-y+2=0相切.
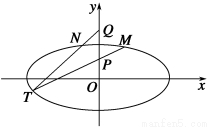
(1)求椭圆C的方程;
(2)已知点P(0,1),Q(0,2),设M,N是椭圆C上关于y轴对称的不同两点,直线PM与QN相交于点T.求证:点T在椭圆C上.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(解析版) 题型:选择题
若-9,a,-1成等差数列,-9,m,b,n,-1成等比数列,则ab=( ).
A.15 B.-15 C.±15 D.10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com