
【题目】某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
文艺节目 | 新闻节目 | 总计 | |
20至40岁 | 30 | 18 | 48 |
大于40岁 | 20 | 32 | 52 |
总计 | 50 | 50 | 100 |
(1)用分层抽样方法在收看文艺节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?
(2)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为大于40岁的概率.
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】已知平面内两个定点![]() 和点
和点![]() ,
,![]() 是动点,且直线
是动点,且直线![]() ,
,![]() 的斜率乘积为常数
的斜率乘积为常数![]() ,设点
,设点![]() 的轨迹为
的轨迹为![]() .
.
① 存在常数![]() ,使
,使![]() 上所有点到两点
上所有点到两点![]() 距离之和为定值;
距离之和为定值;
② 存在常数![]() ,使
,使![]() 上所有点到两点
上所有点到两点![]() 距离之和为定值;
距离之和为定值;
③ 不存在常数![]() ,使
,使![]() 上所有点到两点
上所有点到两点![]() 距离差的绝对值为定值;
距离差的绝对值为定值;
④ 不存在常数![]() ,使
,使![]() 上所有点到两点
上所有点到两点![]() 距离差的绝对值为定值.
距离差的绝对值为定值.
其中正确的命题是_______________.(填出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() )与双曲线
)与双曲线![]() (
(![]() ,
,![]() )有相同的焦点
)有相同的焦点![]() ,点
,点![]() 是两条曲线的一个交点,且
是两条曲线的一个交点,且![]() 轴,则该双曲线经过一、三象限的渐近线的倾斜角所在的区间是( )
轴,则该双曲线经过一、三象限的渐近线的倾斜角所在的区间是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 上的最大值为9,最小值为1,记
上的最大值为9,最小值为1,记![]()
(1)求实数![]() ,
,![]() 的值;
的值;
(2)若不等式![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)定义在![]() 上的函数
上的函数![]() ,设
,设![]() ,
,![]() 将区间
将区间![]() 任意划分成
任意划分成![]() 个小区间,如果存在一个常数
个小区间,如果存在一个常数![]() ,使得和式
,使得和式![]() 恒成立,则称函数
恒成立,则称函数![]() 为在
为在![]() 上的有界变差函数.试判断函数
上的有界变差函数.试判断函数![]() 是否为在
是否为在![]() 上的有界变差函数?若是,求
上的有界变差函数?若是,求![]() 的最小值;若不是,请说明理由(
的最小值;若不是,请说明理由(![]() 表示
表示![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四边形![]() 为矩形,
为矩形, ![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,得到四棱锥
折起,得到四棱锥![]() ,设
,设![]() 的中点为
的中点为![]() ,在翻折过程中,得到如下有三个命题:
,在翻折过程中,得到如下有三个命题:
①![]() 平面
平面![]() ,且
,且![]() 的长度为定值
的长度为定值![]() ;
;
②三棱锥![]() 的最大体积为
的最大体积为![]() ;
;
③在翻折过程中,存在某个位置,使得![]() .
.
其中正确命题的序号为__________.(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面是菱形的四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=60°,PA=AB=2,点E,F分别为BC,PD的中点,设直线PC与平面AEF交于点Q.
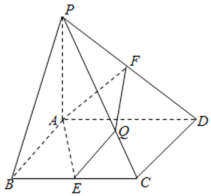
(1)已知平面PAB∩平面PCD=l,求证:AB∥l.
(2)求直线AQ与平面PCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个玩具盘由一个直径为2米的半圆O和一个矩形ABCD构成,![]() 米,如图所示.小球从A点出发以5 V的速度沿半圆O轨道滚到某点E处后,经弹射器以6 V的速度沿与点E切线垂直的方向弹射到落袋区BC内,落点记为F.设
米,如图所示.小球从A点出发以5 V的速度沿半圆O轨道滚到某点E处后,经弹射器以6 V的速度沿与点E切线垂直的方向弹射到落袋区BC内,落点记为F.设![]() 弧度,小球从A到F所需时间为T.
弧度,小球从A到F所需时间为T.
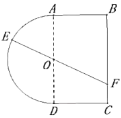
(1)试将T表示为![]() 的函数
的函数![]() ,并写出定义域;
,并写出定义域;
(2)当![]() 满足什么条件时,时间T最短.
满足什么条件时,时间T最短.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com