
【题目】在四棱锥![]() 中,底面
中,底面![]() 为菱形,侧面
为菱形,侧面![]() 为等边三角形,且侧面
为等边三角形,且侧面![]() 底面
底面![]() ,
,![]() ,
,![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.
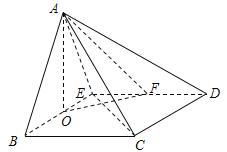
(1)求证:![]() ;
;
(2)求证:平面![]() 平面
平面![]() .
.
【答案】(1)详见解析(2)详见解析
【解析】
试题分析:(1)立体中证明线线垂直,一般利用线面垂直性质定理,即先转化为证明线面垂直,而线面垂直的证明,往往从两个方面进行,一是结合平几知识寻找线线垂直,如利用等边三角形性质得中线垂直底边,另一方面,结合立几中面面垂直条件,将其转化为线面垂直,再得线线垂直(2)证明面面垂直,实质为证明线面垂直,而线面垂直的证明,往往从两个方面进行,一是结合平几知识寻找线线垂直,如利用等边三角形性质得中线垂直底边,另一方面,结合立几中线面垂直条件得线线垂直
试题解析:证明:(1)因为△![]() 为等边三角形,
为等边三角形,![]() 为
为![]() 的中点,
的中点,
所以![]() .
.
又因为平面![]() 面
面![]() ,平面
,平面![]() 面
面![]()
![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,
,
所以![]() .
.
(2)连接![]() ,因为四边形
,因为四边形![]() 为菱形,
为菱形,
所以![]() .
.
因为![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,
所以![]() ,所以
,所以![]() .
.
由(1)可知,![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]()


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:
【题目】已知直线l的方程是y=2x+3,则l关于y=-x对称的直线方程是( )
A. x-2y+3=0 B. x-2y=0
C. x-2y-3=0 D. 2x-y=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列不具有相关关系的是( )
A. 单产不为常数时,土地面积和总产量
B. 人的身高与体重
C. 季节与学生的学习成绩
D. 学生的学习态度与学习成绩
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点.
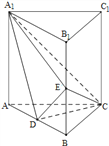
(Ⅰ)证明:BC1∥平面A1CD;
(Ⅱ)AA1=AC=CB=2,AB=![]() ,求三棱锥C﹣A1DE的体积.
,求三棱锥C﹣A1DE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={1,2,4},B={x|x2-4x+m=0}.若A∩B={1},则B=( )
A. {1,-3} B. {1,0}
C. {1,3} D. {1,5}
查看答案和解析>>
科目:高中数学 来源: 题型:
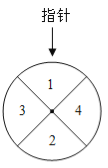
【题目】某儿童乐园在“六一”儿童节推出了一项趣味活动,参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数,设两次记录的数分别为x,y.
奖励规则如下:
①若![]() ,则奖励玩具一个;
,则奖励玩具一个;
②若![]() ,则奖励水杯一个;
,则奖励水杯一个;
③其余情况奖励饮料一瓶.
假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动.
(I)求小亮获得玩具的概率;
(II)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】口袋内装有大小相同的红球、白球和黑球,从中摸出一个球,摸出红球的概率是0.42,摸出白球的概率是0.28,则摸出黑球的概率是( )
A. 0.42 B. 0.28 C. 0.7 D. 0.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一医用放射性物质原来质量为a,每年衰减的百分比相同,当衰减一半时,所用时间是10年,根据需要,放射性物质至少要保留原来的,否则需要更换.已知到今年为止,剩余的为原来的![]() ,
,
(1)求每年衰减的百分比;
(2)到今年为止,该放射性物质已衰减了多少年?
(3)今后至多还能用多少年?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com