Question

【题目】如图，直三棱柱ABC－A1B1C1中，D、E分别是AB、BB1的中点．

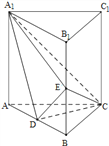
（Ⅰ）证明：BC1∥平面A1CD；

（Ⅱ）AA1＝AC＝CB＝2，AB＝，求三棱锥C﹣A1DE的体积．

Answer 1

【答案】（1）详见解析（2）1

【解析】试题分析：（Ⅰ）连接AC1交A1C于点F，则DF为三角形ABC1的中位线，故DF∥BC1．再根据直线和平面平行的判定定理证得BC1∥平面A1CD．（Ⅱ）由题意可得此直三棱柱的底面ABC为等腰直角三角形，由D为AB的中点可得CD⊥平面ABB1A1．求得CD的值，利用勾股定理求得A1D、DE和A1E的值，可得A1D⊥DE．进而求得S△A1DE的值，再根据三棱锥C-A1DE的体积为S△A1DECD，运算求得结果

试题解析：（1）证明：连结AC1交A1C于点F，则F为AC1中点又D是AB中点，

连结DF，则BC1∥DF． 3分

因为DF平面A1CD，BC1不包含于平面A1CD， 4分

所以BC1∥平面A1CD． 5分

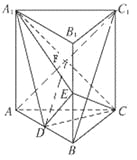
（2）解：因为ABC﹣A1B1C1是直三棱柱，所以AA1⊥CD．由已知AC=CB，D为AB的中点，所以CD⊥AB．又AA1∩AB=A，于是CD⊥平面ABB1A1． 8分

由AA1=AC=CB=2，得∠ACB=90°，，，，A1E=3，故A1D2+DE2=A1E2，即DE⊥A1D 10分

所以三菱锥C﹣A1DE的体积为：==1． 12分