练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若函数f(x)＝x3－x2＋ax＋4恰在[－1,4]上单调递减，则实数a的值为________．


    －4


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如果一个点是一个指数函数和一个对数函数的图象的交点，那么称这个点为“好点”．下列四个点P1(1,1)，P2(1,2)，P3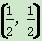，P4(2,2)中，“好点”的个数为(　　)

    A．1                                    B．2

    C．3                                    D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某类产品按工艺共分10个档次，最低档次产品每件利润为8元．每提高一个档次，每件利润增加2元．用同样工时，可以生产最低档产品60件，每提高一个档次将少生产3件产品．则获得利润最大时生产产品的档次是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝x3＋(1－a)x2－a(a＋2)x＋b(a，b∈R)．

    (1)若函数f(x)的图象过原点，且在原点处的切线斜率为－3，求a，b的值．

    (2)若曲线y＝f(x)存在两条垂直于y轴的切线，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)在定义域R内可导，若f(x)＝f(2－x)，且当x∈(－∞，1)时，(x－1)f′(x)<0，设a＝f(0)，b＝f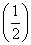，c＝f(3)，则(　　)

    A．a<b<c                                B．c<b<a

    C．c<a<b                                D．b<c<a

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    对于在R上可导的任意函数f(x)，若满足(x－a)f′(x)≥0，则必有(　　)

    A．f(x)≥f(a)                           B．f(x)≤f(a)

    C．f(x)>f(a)                            D．f(x)<f(a)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)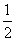＝x2－cosx，x∈[－1,1]，则导函数f′(x)是(　　)

    A．仅有最小值的奇函数

    B．既有最大值，又有最小值的偶函数

    C．仅有最大值的偶函数

    D．既有最大值，又有最小值的奇函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)为定义在(－∞，＋∞)上的可导函数，且f(x)<f′(x)，对于任意x∈R恒成立，则(　　)

    A．f(2)>e2·f(0)，f(2 010)>e2 010·f(0)

    B．f(2)<e2·f(0)，f(2 010)>e2 010·f(0)

    C．f(2)>e2·f(0)，f(2 010)<e2 010·f(0)

    D．f(2)<e2·f(0)，f(2 010)<e2 010·f(0)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若cosθ＋sinθ＝－，则cos的值为(　　)

    A.                                    B.

    C．－                                 D．－

    查看答案和解析>>

    同步练习册答案