
已知f(x)=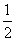 x2-cosx,x∈[-1,1],则导函数f′(x)是( )
x2-cosx,x∈[-1,1],则导函数f′(x)是( )
A.仅有最小值的奇函数
B.既有最大值,又有最小值的偶函数
C.仅有最大值的偶函数
D.既有最大值,又有最小值的奇函数
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
已知函数f(x)=x2的图象在点A(x1,f(x1))与点B(x2,f(x2))处的切线互相垂直,并交于点P,则点P的坐标可能是( )
A.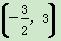 B.(0,-4)
B.(0,-4)
C.(2,3) D.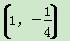
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=ax+x2-xlna-b(a,b∈R,a>1),e是自然对数的底数.
(1)试判断函数f(x)在区间(0,+∞)上的单调性;
(2)当a=e,b=4时,求整数k的值,使得函数f(x)在区间(k,k+1)上存在零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=ax3+x2+bx(a、b为常数),g(x)=f(x)+f′(x)是奇函数.
(1)求f(x)的表达式;
(2)讨论g(x)的单调性,并求g(x)在区间[1,2]上的最大值、最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知y=f(x)是奇函数,当x∈(0,2)时,f(x)=lnx-ax ,当x∈(-2,0)时,f(x)的最小值为1,则a的值等于( )
,当x∈(-2,0)时,f(x)的最小值为1,则a的值等于( )
A.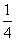 B.
B.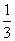
C.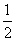 D.1
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y=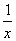 (x>0)图象下方的区域(阴影部分),从D内随机取一个点M,则点M取自E内的概率为( )
(x>0)图象下方的区域(阴影部分),从D内随机取一个点M,则点M取自E内的概率为( )
A.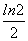 B
B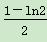
C.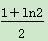 D.
D.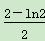

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com