
【题目】已知函数![]() ,
,![]() .
.
![]() 求
求![]() 在
在![]() 上的最小值;
上的最小值;
![]() 若m为整数,当
若m为整数,当![]() 时,
时,![]() 恒成立,求m的最大值.
恒成立,求m的最大值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
![]() 求出函数的导函数,讨论m的取值,研究函数在
求出函数的导函数,讨论m的取值,研究函数在![]() 上的单调性进行求解即可得到结论.
上的单调性进行求解即可得到结论.![]() 把当
把当![]() 时
时![]() 恒成立,转化为
恒成立,转化为![]() ,构造函数
,构造函数![]() ,利用导数求得函数
,利用导数求得函数![]() 的最小值的范围得答案.
的最小值的范围得答案.
![]() 函数的导数
函数的导数![]() ,
,
由![]() 得
得![]() ,
,
由![]() 得
得![]() ,此时函数
,此时函数![]() 为增函数,
为增函数,
由![]() 得
得![]() ,此时函数
,此时函数![]() 为减函数,
为减函数,
即当![]() 时,函数取得极小值,
时,函数取得极小值,![]() ,.
,.
若![]() 即
即![]() 时,函数
时,函数![]() 在
在![]() 上是增函数,此时函数的最小值为
上是增函数,此时函数的最小值为![]() ,
,
若![]() 即
即![]() 时,函数
时,函数![]() 在
在![]() 上是减函数,此时函数的最小值为
上是减函数,此时函数的最小值为![]() ,
,
若![]() ,即
,即![]() 时,函数的最小值为
时,函数的最小值为![]() ;
;
![]() 当
当![]() 时,
时,![]() ,
,
![]() 不等式
不等式![]() ,等价为
,等价为![]() ,即
,即![]()
![]()
令![]() ,则
,则![]() ,
,
函数![]() 在
在![]() 上单调递增,而
上单调递增,而![]() ,
,![]() ,
,
![]() 在
在![]() 上存在唯一的零点,
上存在唯一的零点,
故![]() 在
在![]() 上存在唯一的零点.
上存在唯一的零点.
设此零点为a,则![]() .
.
当![]() ;当
;当![]() 时,
时,![]() ;
;
![]() 在
在![]() 上的最小值为
上的最小值为![]() 由
由![]() ,可得
,可得![]() ,
,
![]() ,
,
由于![]() 式等价于
式等价于![]() ,
,
故整数m的最大值为2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,SA⊥底面ABCD,底面ABCD是平行四边形,E是线段SD上一点.
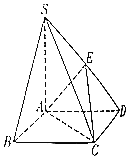
(1)若E是SD的中点,求证:SB∥平面ACE;
(2)若SA=AB=AD=2,SC=2![]() ,且DE
,且DE![]() DS,求二面角S﹣AC﹣E的余弦值.
DS,求二面角S﹣AC﹣E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, 在四棱锥![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
,![]() ,
, ![]() ,
,![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.
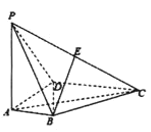
(1)证明:![]() :
:
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)若![]() 为棱
为棱![]() 上一点, 满足
上一点, 满足![]() , 求二面角
, 求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了比较注射![]() ,
,![]() 两种药物后产生的皮肤疱疹的面积,选200只家兔做试验,将这200只家兔随机地分成两组,每组100只,其中一组注射药物
两种药物后产生的皮肤疱疹的面积,选200只家兔做试验,将这200只家兔随机地分成两组,每组100只,其中一组注射药物![]() ,另一组注射药物
,另一组注射药物![]() .下表1和表2分别是注射药物
.下表1和表2分别是注射药物![]() 和药物
和药物![]() 的试验结果.(疱疹面积单位:
的试验结果.(疱疹面积单位:![]() )
)
表1:注射药物![]() 后皮肤疱疹面积的频数分布表
后皮肤疱疹面积的频数分布表
疱疹面积 |
|
|
|
|
频数 | 30 | 40 | 20 | 10 |
表2:注射药物![]() 后皮肤疱疹面积的频数分布表
后皮肤疱疹面积的频数分布表
疱疹面积 |
|
|
|
|
|
频数 | 10 | 25 | 20 | 30 | 15 |
附: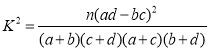
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
(1)完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小(不必算出中位数);
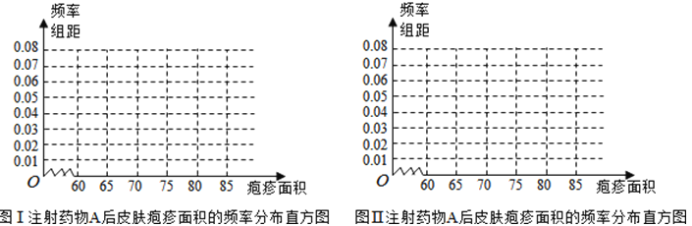
(2)完成下面![]() 列联表,并回答能否有99.9%的把握认为“注射药物
列联表,并回答能否有99.9%的把握认为“注射药物![]() 后的疱疹面积与注射药物
后的疱疹面积与注射药物![]() 后的疱疹面积有差异”.
后的疱疹面积有差异”.
表3:
疱疹面积小于 | 疱疹面积不小于 | 合计 | |
注射药物 |
|
| |
注射药物 |
|
| |
合计 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设三角形的边长为不相等的整数,且最大边长为n,这些三角形的个数为an.
(1)求数列{an}的通项公式;
(2)在1,2,…,100中任取三个不同的整数,求它们可以是一个三角形的三条边长的概率.
附:1+22+32+…+n2![]() ;1+23+33+…+n3
;1+23+33+…+n3![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,将曲线
为参数,将曲线![]() 经过伸缩变换
经过伸缩变换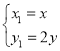 后得到曲线
后得到曲线![]() .在以原点为极点,
.在以原点为极点,![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)说明曲线![]() 是哪一种曲线,并将曲线
是哪一种曲线,并将曲线![]() 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)已知点![]() 是曲线
是曲线![]() 上的任意一点,又直线
上的任意一点,又直线![]() 上有两点
上有两点![]() 和
和![]() ,且
,且![]() ,又点
,又点![]() 的极角为
的极角为![]() ,点
,点![]() 的极角为锐角.求:
的极角为锐角.求:
①点![]() 的极角;
的极角;
②![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】七巧板是一种古老的中国传统智力玩具,顾名思义,是由七块板组成的.而这七块板可拼成许多图形.如图中的正方形七巧板就是由五块等腰直角三角形、一块正方形和一块平行四边形组成的.若向正方形内随机的抛10000颗小米粒(大小忽略不计),则落在阴影部分的小米粒大约为( )
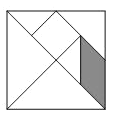
A.3750B.2500C.1875D.1250
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com