
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,将曲线
为参数,将曲线![]() 经过伸缩变换
经过伸缩变换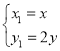 后得到曲线
后得到曲线![]() .在以原点为极点,
.在以原点为极点,![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)说明曲线![]() 是哪一种曲线,并将曲线
是哪一种曲线,并将曲线![]() 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)已知点![]() 是曲线
是曲线![]() 上的任意一点,又直线
上的任意一点,又直线![]() 上有两点
上有两点![]() 和
和![]() ,且
,且![]() ,又点
,又点![]() 的极角为
的极角为![]() ,点
,点![]() 的极角为锐角.求:
的极角为锐角.求:
①点![]() 的极角;
的极角;
②![]() 面积的取值范围.
面积的取值范围.
【答案】(1)曲线![]() 为圆心在原点,半径为2的圆.
为圆心在原点,半径为2的圆.![]() 的极坐标方程为
的极坐标方程为![]() (2)①
(2)①![]() ②
②
【解析】
(1)求得曲线![]() 伸缩变换后所得
伸缩变换后所得![]() 的参数方程,消参后求得
的参数方程,消参后求得![]() 的普通方程,判断出
的普通方程,判断出![]() 对应的曲线,并将
对应的曲线,并将![]() 的普通方程转化为极坐标方程.
的普通方程转化为极坐标方程.
(2)
①将![]() 的极角代入直线
的极角代入直线![]() 的极坐标方程,由此求得点
的极坐标方程,由此求得点![]() 的极径,判断出
的极径,判断出![]() 为等腰三角形,求得直线
为等腰三角形,求得直线![]() 的普通方程,由此求得
的普通方程,由此求得![]() ,进而求得
,进而求得![]() ,从而求得点
,从而求得点![]() 的极角.
的极角.
②解法一:利用曲线![]() 的参数方程,求得曲线
的参数方程,求得曲线![]() 上的点
上的点![]() 到直线
到直线![]() 的距离
的距离![]() 的表达式,结合三角函数的知识求得
的表达式,结合三角函数的知识求得![]() 的最小值和最大值,由此求得
的最小值和最大值,由此求得![]() 面积的取值范围.
面积的取值范围.
解法二:根据曲线![]() 表示的曲线,利用圆的几何性质求得圆
表示的曲线,利用圆的几何性质求得圆![]() 上的点到直线
上的点到直线![]() 的距离的最大值和最小值,进而求得
的距离的最大值和最小值,进而求得![]() 面积的取值范围.
面积的取值范围.
(1)因为曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),
因为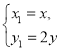 则曲线
则曲线![]() 的参数方程
的参数方程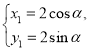
所以![]() 的普通方程为
的普通方程为![]() .所以曲线
.所以曲线![]() 为圆心在原点,半径为2的圆.
为圆心在原点,半径为2的圆.
所以![]() 的极坐标方程为
的极坐标方程为![]() ,即
,即![]() .
.
(2)①点![]() 的极角为
的极角为![]() ,代入直线
,代入直线![]() 的极坐标方程
的极坐标方程![]() 得点
得点![]()
极径为![]() ,且
,且![]() ,所以
,所以![]() 为等腰三角形,
为等腰三角形,
又直线![]() 的普通方程为
的普通方程为![]() ,
,
又点![]() 的极角为锐角,所以
的极角为锐角,所以![]() ,所以
,所以![]() ,
,
所以点![]() 的极角为
的极角为![]() .
.
②解法1:直线![]() 的普通方程为
的普通方程为![]() .
.
曲线![]() 上的点
上的点![]() 到直线
到直线![]() 的距离
的距离
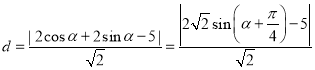 .
.
当![]() ,即
,即![]() (
(![]() )时,
)时,
![]() 取到最小值为
取到最小值为![]() .
.
当![]() ,即
,即![]() (
(![]() )时,
)时,
![]() 取到最大值为
取到最大值为![]() .
.
所以![]() 面积的最大值为
面积的最大值为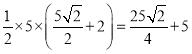 ;
;
所以![]() 面积的最小值为
面积的最小值为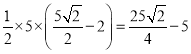 ;
;
故![]() 面积的取值范围
面积的取值范围 .
.
解法2:直线![]() 的普通方程为
的普通方程为![]() .
.
因为圆![]() 的半径为2,且圆心到直线
的半径为2,且圆心到直线![]() 的距离
的距离![]() ,
,
因为![]() ,所以圆
,所以圆![]() 与直线
与直线![]() 相离.
相离.
所以圆![]() 上的点
上的点![]() 到直线
到直线![]() 的距离最大值为
的距离最大值为![]() ,
,
最小值为![]() .
.
所以![]() 面积的最大值为
面积的最大值为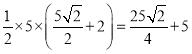 ;
;
所以![]() 面积的最小值为
面积的最小值为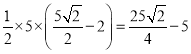 ;
;
故![]() 面积的取值范围
面积的取值范围 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为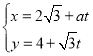 (其中t为参数),以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,点A的极坐标为
(其中t为参数),以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,点A的极坐标为![]() ,直线
,直线![]() 经过点A.曲线C的极坐标方程为
经过点A.曲线C的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线C的直角坐标方程;
的普通方程与曲线C的直角坐标方程;
(2)过点![]() 作直线
作直线![]() 的垂线交曲线C于D,E两点(D在x轴上方),求
的垂线交曲线C于D,E两点(D在x轴上方),求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
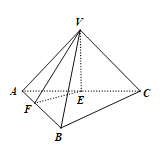
【题目】如图,三棱锥![]() 的侧棱长都相等,底面
的侧棱长都相等,底面![]() 与侧面
与侧面![]() 都是以
都是以![]() 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为直线
为直线![]() 上的动点,若平面
上的动点,若平面![]() 与平面
与平面![]() 所成锐二面角的平面角为
所成锐二面角的平面角为![]() ,则
,则![]() 的最大值是( )
的最大值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中盈不足章中有这样一则故事:“今有良马与驽马发长安,至齐. 齐去长安三千里. 良马初日行一百九十三里,日增一十二里;驽马初日行九十七里,日减二里.” 为了计算每天良马和驽马所走的路程之和,设计框图如下图. 若输出的 ![]() 的值为 350,则判断框中可填( )
的值为 350,则判断框中可填( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有如下命题:①若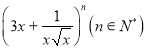 的展开式中含有常数项,且
的展开式中含有常数项,且![]() 的最小值为
的最小值为![]() ;②
;②![]() ;③若有一个不透明的袋子内装有大小、质量相同的
;③若有一个不透明的袋子内装有大小、质量相同的![]() 个小球,其中红球有
个小球,其中红球有![]() 个,白球有
个,白球有![]() 个,每次取一个,取后放回,连续取三次,设随机变量
个,每次取一个,取后放回,连续取三次,设随机变量![]() 表示取出白球的次数,则
表示取出白球的次数,则![]() ;④若定义在R上的函数
;④若定义在R上的函数![]() 满足
满足![]() ,则
,则![]() 的最小正周期为
的最小正周期为![]() ;
;
则正确论断有______________.(填写序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
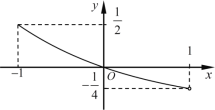
【题目】函数![]() 的定义域为
的定义域为![]() ,其图象如图所示.函数
,其图象如图所示.函数![]() 是定义域为
是定义域为![]() 的奇函数,满足
的奇函数,满足![]() ,且当
,且当![]() 时,
时,![]() .给出下列三个结论:
.给出下列三个结论:
①![]() ;
;
②函数![]() 在
在![]() 内有且仅有
内有且仅有![]() 个零点;
个零点;
③不等式![]() 的解集为
的解集为![]() .
.
其中,正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对两个变量![]() 与
与![]() 进行线性相关性和回归效果分析,得到一组样本数据:
进行线性相关性和回归效果分析,得到一组样本数据:![]() 、
、![]() 、
、![]() 、
、![]() ,则下列说法不正确的是( )
,则下列说法不正确的是( )
A.残差平方和越小的模型,拟合的效果越好
B.由样本数据利用最小二乘法得到的回归方程表示的直线必过样本点的中心![]()
C.若变量![]() 与
与![]() 之间的相关系数
之间的相关系数![]() ,则变量
,则变量![]() 与
与![]() 之间具有很强的线性相关性
之间具有很强的线性相关性
D.用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越小,说明模型的拟合效果越好
越小,说明模型的拟合效果越好
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com