
【题目】如图,在这个正方体中,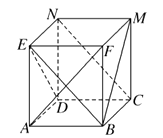
① ![]() 与
与 ![]() 平行;
平行;
② ![]() 与
与 ![]() 是异面直线;
是异面直线;
③ ![]() 与
与 ![]() 是异面直线;
是异面直线;
④ ![]() 与
与 ![]() 是异面直线;
是异面直线;
以上四个命题中,正确命题的序号是 .
科目:高中数学 来源: 题型:
【题目】已知结论:“在三边长都相等的△ABC中,若D是BC的中点,G是△ABC外接圆的圆心,则 ![]() ”.若把该结论推广到空间,则有结论:“在六条棱长都相等的四面体ABCD中,若M是△BCD的三边中线的交点,O为四面体ABCD外接球的球心,则
”.若把该结论推广到空间,则有结论:“在六条棱长都相等的四面体ABCD中,若M是△BCD的三边中线的交点,O为四面体ABCD外接球的球心,则 ![]() = .
= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥 ![]() 中,侧面
中,侧面 ![]() 底面
底面 ![]() ,侧棱
,侧棱 ![]() ,底面
,底面 ![]() 为直角梯形,其中
为直角梯形,其中 ![]() 为
为 ![]() 中点.
中点.
(1)求证: ![]() 平面
平面 ![]() ;
;
(2)求异面直线 ![]() 与
与 ![]() 所成角的余弦值;
所成角的余弦值;
(3)线段 ![]() 上是否存在
上是否存在 ![]() ,使得它到平面
,使得它到平面 ![]() 的距离为
的距离为 ![]() ?若存在,求出
?若存在,求出 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(其中x∈R,A>0,ω>0, ![]() )的部分图象如图所示
)的部分图象如图所示 
(Ⅰ)求A,ω,φ的值;
(Ⅱ)求f(x)的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣ax+a2﹣19=0},集合B={x|x2﹣5x+6=0},C={x|x2+2x﹣8=0}.
(1)若A∩B=A∪B,求a的值;
(2)若A∩B,A∩C=,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为做好2022年北京冬季奥运会的宣传工作,组委会计划从某大学选取若干大学生志愿者,某记者在该大学随机调查了1000名大学生,以了解他们是否愿意做志愿者工作,得到的数据如表所示:
愿意做志愿者工作 | 不愿意做志愿者工作 | 合计 | |
男大学生 | 610 | ||
女大学生 | 90 | ||
合计 | 800 |
(1)根据题意完成表格;
(2)是否有95%的把握认为愿意做志愿者工作与性别有关? 参考公式及数据: ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥K0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
K0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com