【题目】已知在平面直角坐标系中，圆
的参数方程为
（
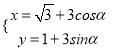为参数），以原点为极点，以
轴为非负半轴为极轴建立极坐标系.
（1）求圆
的普通方程与极坐标方程；
（2）若直线
的极坐标方程为
，求圆
上的点到直线
的最大距离.
科目：高中数学 来源： 题型：
【题目】哈三中群力校区高二、六班同学用随机抽样的办法对所在校区老师的饮食习惯进行了一次调查, 饮食指数结果用茎叶图表示如图, 图中饮食指数低于70的人，饮食以蔬菜为主；饮食指数高于70的人，饮食以肉类为主.
(1)完成下列
列联表：
能否有
的把握认为老师的饮食习惯与年龄有关？
(2)从调查的结果中饮食指数在
的老师内任选3名老师, 设“选到的三位老师饮食指数之和不超过105”为事件
, 求事件发生的概率；
(3)为了给食堂提供老师的饮食信息, 根据(1)的结论，能否有更好的抽样方法来估计老师的饮食习惯, 并说明理由.
附:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某赛季甲、乙两名篮球运动员每场比赛得分的原始记录如下：
甲运动员得分：13,51,23,8,26,38,16,33,14,28,39；
乙运动员得分：49,24,12，31,50,31,44,36,15,37,25,36,39.
(1)用十位数为茎，在答题卡中画出原始数据的茎叶图；
(2)用分层抽样的方法在乙运动员得分十位数为 2,3,4 的比赛中抽取一个容量为 5 的样本，从该样本中随机抽取 2 场，求其中恰有 1 场得分大于 40 分的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆
，直线
.
（1）求证：对
，直线
与圆
总有两个交点；
（2）设直线与圆交于点
，若
，直线的倾斜角；
（3）设直线与圆交于点，若定点
满足
，求此时直线的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆
，圆
过
作圆
的切线，切点为
（在第二象限）.
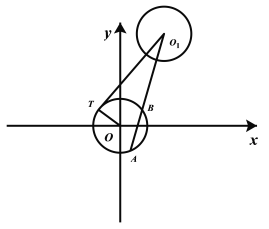
（1）求
的正弦值；
（2）已知点
，过
点分别作两圆切线，若切线长相等，求
关系；
（3）是否存在定点
，使过点
有无数对相互垂直的直线
满足
，且它们分别被圆、圆所截得的弦长相等？若存在，求出所有的点；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥P-ABCD中，底面ABCD是正方形，
平面ABCD，且
，点E为线段PD的中点.
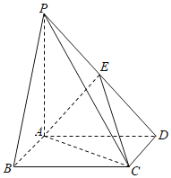
（1）求证：
平面AEC；
（2）求证：
平面PCD；
（3）求三棱锥
的体积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】语音交互是人工智能的方向之一，现在市场上流行多种可实现语音交互的智能音箱，它们可以通过语音交互满足人们的部分需求.经市场调查，某种新型智能音箱的广告费支出x（万元）与销售额y（单位：万元）之间有如下对应数据：
x | 1 | 4 | 5 | 6 | 9 |
y | 20 | 35 | 50 | 65 | 80 |
（1）求y关于x的线性回归方程（数据精确到0.01）；
（2）利用（1）中的回归方程，预测广告费支出10万元时的销售额.
附：回归直线的斜率和截距的最小二乘估计公式分别为：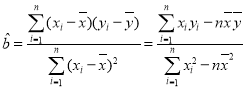
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数
， 
.
（1）若函数
在
上单调递增，求
的取值范围；
（2）设
，点
是曲线
与
的一个交点，且这两曲线在点
处的切线互相垂直，证明：存在唯一的实数
满足题意，且
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
