
 已知f(x)是定义在R上的偶函数,且当x≤0时,f(x)=2x+1+l.
已知f(x)是定义在R上的偶函数,且当x≤0时,f(x)=2x+1+l.分析 (1)由条件利用函数的奇偶性求函数的解析式.
(2)由题意可得f(x)=$\frac{m+1}{2}$恰有两个不同实根,即函数f(x)的图象和直线y=$\frac{m+1}{2}$恰有两个不同的交点,数形结合可得m的范围.
解答 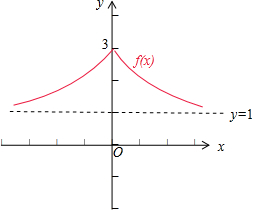 解:(1)设x>0,则-x<0,∵当x≤0时,f(x)=2x+1+l,
解:(1)设x>0,则-x<0,∵当x≤0时,f(x)=2x+1+l,
∴f(-x)=21-x+1=f(x),∴f(x)=21-x+1.
综上可得,f(x)=$\left\{\begin{array}{l}{{2}^{x+1}+1,x≤0}\\{{2}^{-x+1}+1,x>0}\end{array}\right.$
(2)在所给的坐标系内画出函数f(x)的草图,如图所示:
方程2f(x)-m-l=0恰有两个不同实根,即f(x)=$\frac{m+1}{2}$恰有两个不同实根,
即函数f(x)的图象和直线y=$\frac{m+1}{2}$恰有两个不同的交点,
故有1<$\frac{m+1}{2}$<3,求得3<m<7,即实数m的取值范围为(3,7).
点评 本题主要考查利用函数的奇偶性求函数的解析式,方程根的存在性以及个数判断,体现了转化、数形结合的数学思想,属于中档题.


科目:高中数学 来源: 题型:解答题
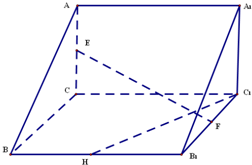 直三棱柱A1B1C1-ABC,$∠ACB=\frac{π}{2},AC=BC=2,C{C_1}=2\sqrt{2}$,E,F,H为AC,B1C1,BB1的中点,
直三棱柱A1B1C1-ABC,$∠ACB=\frac{π}{2},AC=BC=2,C{C_1}=2\sqrt{2}$,E,F,H为AC,B1C1,BB1的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 上午生产情况正常,下午生产情况异常 | |
| B. | 上午生产情况异常,下午生产情况正常 | |
| C. | 上、下午生产情况均正常 | |
| D. | 上、下午生产情况均不正常 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{9}{4}$,0] | B. | [-$\frac{9}{4}$,0) | C. | (-∞,-$\frac{9}{4}$)∪[0,+∞) | D. | (-∞,-$\frac{9}{4}$)∪(0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 时间代号t | 1 | 2 | 3 | 4 | 5 |
| 储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com