
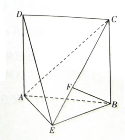
 如图所示,正方形ABCD的边长为2,且平面ABCD⊥平面ABE,AE=BE,F为CE上的点,且BF⊥平面ACE.
如图所示,正方形ABCD的边长为2,且平面ABCD⊥平面ABE,AE=BE,F为CE上的点,且BF⊥平面ACE.分析 (1)推导出BF⊥AE,BC⊥AB,从而BC⊥AE,由此能证明AE⊥平面BCE.
(2)推导出AE=BE=$\sqrt{2}$,CF=$\frac{2\sqrt{6}}{3}$,作EG⊥AB于G,FH⊥面ABCD,EG=1,从而$\frac{EG}{FH}=\frac{EC}{FC}=\frac{3}{2}$,由此能求出FH.
解答 证明:(1)∵BF⊥平面ACE,∴BF⊥AE,
又平面ABCD⊥平面ABE,BC⊥AB,
∴BC⊥平面ABE,∴BC⊥AE,
又BF?平面BCE,BC?平面BCE,BF∩BC=B,
∴AE⊥平面BCE.
解:(2)∵AB=2,∴AE=BE=$\sqrt{2}$,
∴CE=$\sqrt{6}$,BC2=CF•CE,∴CF=$\frac{4}{\sqrt{6}}$=$\frac{2\sqrt{6}}{3}$,
EG⊥AB于G,FH⊥面ABCD,
C、G、H三点共线,又EG=1,
∴$\frac{EG}{FH}=\frac{EC}{FC}=\frac{3}{2}$,∴FH=$\frac{2}{3}$.
点评 本题考查线面垂直的证明,考查线段长的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
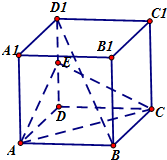 如图,在正方体ABCD-A1B1C1D1中,E为棱DD1的中点,求证:
如图,在正方体ABCD-A1B1C1D1中,E为棱DD1的中点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
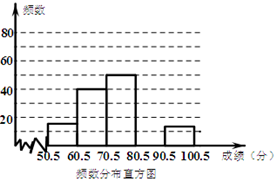 2013年3月28日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计.请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:
2013年3月28日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计.请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:| 分数段 | 频数 | 频率 |
| 50.5~60.5 | 16 | 0.08 |
| 60.5~70.5 | 40 | 0.2 |
| 70.5~80.5 | 50 | 0.25 |
| 80.5~90.5 | m | 0.35 |
| 90.5~100.5 | 24 | n |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com