
| a |
| b |
| c |
| a |
| b |
| c |
| 0 |
| a |
| b |
| 2π |
| 3 |
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:高中数学 来源: 题型:
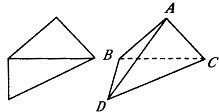 如图是一副直角三角板.现将两三角板拼成直二面角,得到四面体ABCD,则下列叙述中正确的是.
如图是一副直角三角板.现将两三角板拼成直二面角,得到四面体ABCD,则下列叙述中正确的是.| BD |
| AC |
查看答案和解析>>
科目:高中数学 来源: 题型:
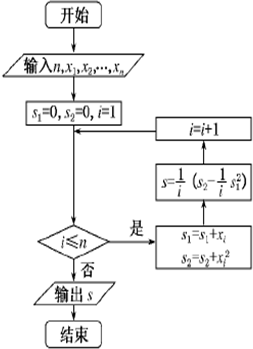 某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中n位居民的月均用水量分别为x1,…,xn(单位:吨).根据如图所示的程序框图,若n=2,且x1,x2分别为1,2,则输出的结果s为
某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中n位居民的月均用水量分别为x1,…,xn(单位:吨).根据如图所示的程序框图,若n=2,且x1,x2分别为1,2,则输出的结果s为查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 2 |
| A、cosθ<tanθ<sinθ |
| B、sinθ<cosθ<tanθ |
| C、tanθ<sinθ<cosθ |
| D、cosθ<sinθ<tanθ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| A、焦点在x轴上的椭圆 |
| B、焦点在x轴上的双曲线 |
| C、焦点在y轴上的椭圆 |
| D、焦点在y轴上的双曲线 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com