
分析 (Ⅰ)记“这2人的累计得分X≤3”的事件为A,事件A的对立事件是“X=5”,
根据相互独立事件的乘法公式求出对立事件的概率,再利用对立事件的概率公式列方程求出P0;
(Ⅱ)设甲、乙两人都选择方案一得分为X1,都选择方案二得分为X2,
计算这两人都选择方案一累计得分的数学期望为E(2X1),
都选择方案二累计得分的数学期望为E(3X2),计算数学期望,比较得出结论.
解答 解:(Ⅰ)由已知得,甲选择方案一,得分的概率为$\frac{2}{3}$,
乙选择方案二,得分的概率为P0,且两人得分与否互不影响;
记“这2人的累计得分X≤3”的事件为A,则事件A的对立事件为“X=5”,
因为P(X=5)=$\frac{2}{3}$×P0,所以P(A)=1-P(X=5)=1-$\frac{2}{3}$×P0=$\frac{7}{9}$,
所以P0=$\frac{1}{3}$;
(Ⅱ)设甲、乙都选择方案一得分为X1,都选择方案二得分为X2,
则这两人选择方案一累计得分的数学期望为E(2X1),
选择方案二累计得分的数学期望为E(3X2);
由已知可得,X1~B(2,$\frac{2}{3}$),X2~B(2,P0),
所以E(X1)=2×$\frac{2}{3}$=$\frac{4}{3}$,E(X2)=2×P0,
从而E(2X1)=2E(X1)=$\frac{8}{3}$,E(3X2)=3E(X2)=6P0;
若E(2X1)>E(3X2),则$\frac{8}{3}$>6P0,所以0<P0<$\frac{4}{9}$;
若E(2X1)<E(3X2),则$\frac{8}{3}$<6P0,所以$\frac{4}{9}$<P0<1;
若E(2X1)=E(3X2),则$\frac{8}{3}$=6P0,所以P0=$\frac{4}{9}$;
综上,0<P0<$\frac{4}{9}$时,选择方案一累计得分的数学期望大;
$\frac{4}{9}$<P0<1时,选择方案二累计得分的数学期望大;
P0=$\frac{4}{9}$时,选择方案一或二,累计得分的数学期望一样大.
点评 本题考查了利用概率知识解决实际问题,以及数学期望的计算问题,确定X服从的分布是解题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
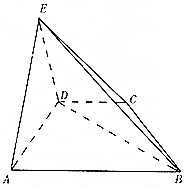 如图,在四棱锥E-ABCD中,△ADE是正三角形,侧面ADE⊥底面ABCD,AB∥DC,BD=2DC=4,AD=3,AB=5.
如图,在四棱锥E-ABCD中,△ADE是正三角形,侧面ADE⊥底面ABCD,AB∥DC,BD=2DC=4,AD=3,AB=5.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
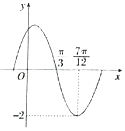 函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的部分图象如图所示,则下列结论:①将f(x)的图象向左平移$\frac{π}{6}$个单位,所得到的函数是偶函数:②f(0)=1;③最小正周期为π;④$f(\frac{12π}{11})<f(\frac{14π}{13})$;⑤$f(x)=-f(\frac{5π}{3}-x)$.其中正确的结论有( )
函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的部分图象如图所示,则下列结论:①将f(x)的图象向左平移$\frac{π}{6}$个单位,所得到的函数是偶函数:②f(0)=1;③最小正周期为π;④$f(\frac{12π}{11})<f(\frac{14π}{13})$;⑤$f(x)=-f(\frac{5π}{3}-x)$.其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com