
分析 由a1a2…an=1得:当n≥2时,a1a2…an-1=1,两个式子相除求出an、$\frac{1}{{a}_{n}}$,代入不等式的左边化简即可证明结论成立.
解答 证明:由题意得,a1a2…an=1,①
所以当n≥2时,a1a2…an-1=1,②
$\frac{①}{②}$得an=1,则$\frac{1}{{a}_{n}}$=1,
所以$\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}}+…+\frac{1}{{a}_{n}}+\frac{3n}{{a}_{1}+{a}_{2}+…+{a}_{n}}$=n+$\frac{3n}{n}$=n+3,
所以$\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}}+…+\frac{1}{{a}_{n}}+\frac{3n}{{a}_{1}+{a}_{2}+…+{a}_{n}}$≥n+3成立.
点评 本题考查数列的递推公式的化简、变形,以及数列与不等式的问题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
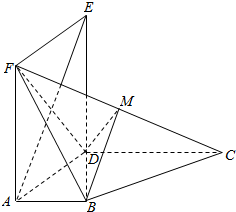 如图所示,平面ADEF⊥平面ABCD,且四边形ADEF为正方形,AD⊥DC,AB∥CD,AB=AD=$\frac{1}{2}$DC=2,M为CE的中点.
如图所示,平面ADEF⊥平面ABCD,且四边形ADEF为正方形,AD⊥DC,AB∥CD,AB=AD=$\frac{1}{2}$DC=2,M为CE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面ABCD是平行四边形,M、N分别是AB、PC的中点,且MN⊥PC,MN⊥AB.证明:平面PAD⊥平面PDC.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,M、N分别是AB、PC的中点,且MN⊥PC,MN⊥AB.证明:平面PAD⊥平面PDC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com