
| ||
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 2 |
| c |
| a |
| ||
| 3 |
| 3 | ||
|
| 3 |
| x2 |
| 3 |
|
| 3m2-3 |
| 1+3k2 |
| -6km |
| 1+3k2 |
| 3m2-3 |
| 1+3k2 |
| -6km |
| 1+3k2 |
| m2-3k2 |
| 1+3k2 |
| OP |
| OQ |
| 4m2-3k2-3 |
| 1+3k2 |
| 3k2+3 |
| 4 |
| |m| | ||
|
|
|
| ||
| 2 |
| OP |
| OQ |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
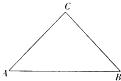 某公司为其中公司成立十五周年,回馈政府的支持和帮助,决定于市中心新建一三角形绿地广场,如图,△ABC为一个等腰三角形性状的绿地,腰CA的长为3(百米),底AB的长为4(百米),现决定在绿地内筑一条笔直的小路EF(宽度不计),将该绿地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为S1和S2.
某公司为其中公司成立十五周年,回馈政府的支持和帮助,决定于市中心新建一三角形绿地广场,如图,△ABC为一个等腰三角形性状的绿地,腰CA的长为3(百米),底AB的长为4(百米),现决定在绿地内筑一条笔直的小路EF(宽度不计),将该绿地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等、面积分别为S1和S2.| S1 |
| S2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| (x+a) |
| (x+a+b)2 |
| (y+c)2 |
| x2 |
| (x+y)2 |
| y2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| an |
| an+1 |
| an-1 |
| an-1 |
| an+1-1 |
| 4 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
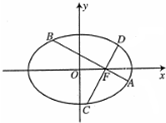 如图,在平面直角坐标系xoy中,椭圆
如图,在平面直角坐标系xoy中,椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 48 |
| 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com