
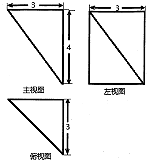
 已知,某几何体的三视图(单位:cm)如图所示,则该几何体的体积为12(cm3);表面积为30+6$\sqrt{2}$(cm2).
已知,某几何体的三视图(单位:cm)如图所示,则该几何体的体积为12(cm3);表面积为30+6$\sqrt{2}$(cm2). 分析 根据已知中的三视图,画出几何体的直观图,进而代入棱锥的体积公式,可得体积,计算每个面的面积,相加可得表面积.
解答 解:解:由三视图可知该几何体为四棱锥V-ABCD,
此四棱锥的底面为矩形,边长分别为3,4,侧棱VA和底面垂直,该棱长为3,即棱锥的高为3,
故体积为:$\frac{1}{3}$×3×12=12cm3;
侧面VAB的面积为:$\frac{1}{2}×3×3=\frac{9}{2}$
侧面VAD的面积为:$\frac{1}{2}$×3×4=6
侧面VBC的面积为:$\frac{1}{2}×3\sqrt{2}×4=6\sqrt{2}$
侧面VCD的面积为:$\frac{1}{2}×3×5=\frac{15}{2}$
故几何体的表面积S=30+6$\sqrt{2}$cm2
故答案为:12,30+6$\sqrt{2}$
点评 本题考查了利用空间几何体的三视图求体积与表面积的应用问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{8}$ | B. | $\frac{7π}{8}$ | C. | $\frac{11π}{8}$ | D. | $\frac{21π}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| X | 6 | 9 | 12 | 18 |
| P | a | $\frac{1}{3}$ | $\frac{1}{10}$ | $\frac{1}{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com