
分析 先求出${S}_{1}={4}^{2}=16$,${S}_{2}=1{0}^{2}=100$,再求出斜率为5,此正棱台的全面积S=S1+S2+$\frac{上下底周长和}{2}$×斜高,体积V=$\frac{1}{3}({S}_{1}+{S}_{2}+\sqrt{{S}_{1}{S}_{2}})•h$,由此能求出结果.
解答 解:∵正棱台的底面是正方形,上底面边长为4cm,下底面边长为10cm,高为4cm,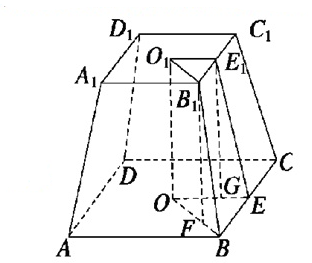
∴${S}_{1}={4}^{2}=16$,${S}_{2}=1{0}^{2}=100$,
如图,O1E1=OG=2,EG=OE-OG=5-2=3,
E1G=O1O=4,
∴E1E=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∴此正棱台的全面积S=S1+S2+$\frac{4×4+4×10}{2}×5$=16+100+140=256(cm2).
∴此正棱台体积V=$\frac{1}{3}({S}_{1}+{S}_{2}+\sqrt{{S}_{1}{S}_{2}})•h$
=$\frac{1}{3}(16+100+\sqrt{16×100})×4$=208(cm3).
点评 本题考查正四棱台的全面积和体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、空间想象能力、运算求解能力,考查函数与方程思想、化归与转化思想、数形结合思想,是中档题.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河南省新乡市高二上学期入学考数学卷(解析版) 题型:选择题
有五条线段长度分别为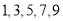 ,从这
,从这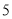 条线段中任取
条线段中任取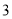 条,则所取
条,则所取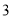 条线段能构成一个三角形的概率为
条线段能构成一个三角形的概率为
A.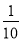 B.
B.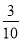 C.
C.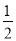 D.
D.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二文上第一次月考数学试卷(解析版) 题型:选择题
某企业有职工150人,其中高级职工15人,中级职工45人,一般职工90人,现抽30人进行分层抽样,则各职称人数分别为( )
A.5,10,15 B.3,9,18
C.3,10,17 D.5,9,16
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | 2-$\frac{2\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
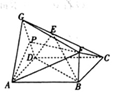 如图所示的多面体中,底面ABCD为正方形,△GAD为等边三角形,∠GDC=90°,点E是线段GC上除两端点外的一点.
如图所示的多面体中,底面ABCD为正方形,△GAD为等边三角形,∠GDC=90°,点E是线段GC上除两端点外的一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k=-2 | B. | $k=\frac{1}{2}$ | C. | k=1 | D. | k=-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com