
| A. | y=($\frac{1}{3}$)1-x | B. | y=x2 | C. | y=5${\;}^{\frac{1}{2-x}}$ | D. | y=$\sqrt{1-{2}^{x}}$ |
分析 根据指数函数的值域,二次函数的值域,以及反比例函数的值域,和被开方数大于等于0,以及不等式的性质便可求出每个选项函数的值域,从而找出正确选项.
解答 解:A.对任意x∈R,$(\frac{1}{3})^{1-x}>0$;
∴该函数值域为(0,+∞),∴该选项正确;
B.y=x2≥0;
∴该函数值域为[0,+∞),∴该选项错误;
C.∵$\frac{1}{2-x}≠0$;
∴${5}^{\frac{1}{2-x}}≠1$;
∴该函数的值域不是(0,+∞),∴该选项错误;
D.$\left\{\begin{array}{l}{{2}^{x}>0}\\{1-{2}^{x}≥0}\end{array}\right.$;
∴0≤1-2x<1;
∴0≤y<1;
即该函数的值域为[0,1),不是(0,+∞),∴该选项错误.
故选:A.
点评 考查函数值域的概念及求法,指数函数、二次函数,及反比例函数的值域,以及被开方数应满足大于等于0,不等式的性质.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:选择题
| A. | $[{\sqrt{2}-1,\sqrt{2}+1}]$ | B. | $[{1,\sqrt{2}+1}]$ | C. | [0,2] | D. | $[{\sqrt{5}-1,\sqrt{5}+1}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 4+2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 图象连续的函数f(x)在区间(a,b)上一定存在最值 | |
| B. | 函数的极小值可能大于极大值 | |
| C. | 函数的最小值一定是极小值 | |
| D. | 函数的极小值一定是最小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
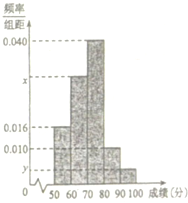 某中学举行了一次“环保知识竞赛”活动,为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出如图所示的频率分布直方图,但由于不慎丢失了部分数据.已知得分在[50,60)的有8人,在[90,100)的有2人,由此推测频率分布直方图中的x=( )
某中学举行了一次“环保知识竞赛”活动,为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出如图所示的频率分布直方图,但由于不慎丢失了部分数据.已知得分在[50,60)的有8人,在[90,100)的有2人,由此推测频率分布直方图中的x=( )| A. | 0.04 | B. | 0.03 | C. | 0.02 | D. | 0.01 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com