已知函数f(x)=x|x2-a|,a∈R.
(Ⅰ)当a≤0时,求证函数f(x)在(-∞,+∞)上是增函数;
(Ⅱ)当a=3时,求函数f(x)在区间[0,b]上的最大值.
【答案】
分析:(1)利用导函数判断函数的单调性.
(2)函数取最值的可能点为极值点,端点,间断点,因此找出这些点,再比较函数值即可.
解答:(Ⅰ)解:∵a≤0,∴x
2-a≥0,∴f(x)=x(x
2-a)=x
3-ax,
∴f
′(x)=3x
2-a,
∵f
′(x)≥0对x∈R成立,
∴函数f(x)在(-∞,+∞)上是增函数.
(Ⅱ)解:当a=3时,f(x)=x|x
2-3|=
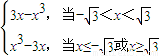
(i)当x<-
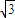
,或x>
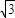
时,f
′(x)=3x
2-3=3(x-1)(x+1)>0.
(ii)当-
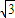
<x<
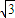
时,f
′(x)=3-3x
2=-3(x-1)(x+1).
当-1<x<1时,f
′(x)>0;
当-
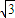
<x<-1,或1<x<
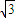
时,f¢(x)<0.
所以f(x)的单调递增区间是(-∞,-
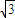
],[-1,1],[
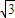
,+∞);
f(x)的单调递减区间是[-
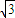
,-1],[1,
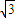
].(8分)
由区间的定义可知,b>0.
①若0<b≤1时,则[0,b]Ì[-1,1],因此函数f(x)在[0,b]上是增函数,
∴当x=b时,f(x)有最大值f(b)=3b-b
3.
②若1<b≤
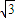
时,f(x)=3x-x
3在[0,1]上单调递增,在[1,b]上单调递减,因此,在x=1时取到极大值f(1)=2,并且该极大值就是函数f(x)在区间[0,b]上的最大值.
∴当x=1时,f(x)有最大值2.
③若b>
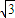
时,当x∈[0,
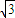
]时,f(x)=3x-x
3在[0,1]上单调递增,在[1,
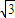
]上单调递减,
因此,在x=1时取到极大值f(1)=2,在x∈[
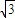
,b]时,f(x)=x
3-3x在[
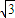
,b]上单调递增,
在x=b时,f(x)有最大值f(b)=b
3-3b.
(i)当f(1)≥f(b),即2≥b
3-3b,b
3-b-2b-2≤0,b(b
2-1)-2(b+1)≤0,(b+1)
2(b-2)≤0,b≤2.
∴当
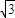
<b≤2时,在x=1时,f(x)取到最大值f(1)=2.
(ii)当f(1)<f(b),解得b>2,
∴当b>2时,f(x)在x=b时,取到最大值f(b)=b
3-3b,
综上所述,函数y=f(x)在区间[0,b]上的最大值为y
max=
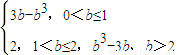
.
点评:本题主要考查了函数的单调性以及函数的最值问题,注意分情况讨论.

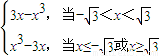
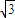 ,或x>
,或x>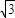 时,f′(x)=3x2-3=3(x-1)(x+1)>0.
时,f′(x)=3x2-3=3(x-1)(x+1)>0.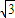 <x<
<x<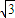 时,f′(x)=3-3x2=-3(x-1)(x+1).
时,f′(x)=3-3x2=-3(x-1)(x+1).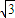 <x<-1,或1<x<
<x<-1,或1<x<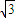 时,f¢(x)<0.
时,f¢(x)<0.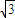 ],[-1,1],[
],[-1,1],[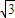 ,+∞);
,+∞);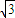 ,-1],[1,
,-1],[1,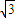 ].(8分)
].(8分)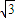 时,f(x)=3x-x3在[0,1]上单调递增,在[1,b]上单调递减,因此,在x=1时取到极大值f(1)=2,并且该极大值就是函数f(x)在区间[0,b]上的最大值.
时,f(x)=3x-x3在[0,1]上单调递增,在[1,b]上单调递减,因此,在x=1时取到极大值f(1)=2,并且该极大值就是函数f(x)在区间[0,b]上的最大值.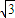 时,当x∈[0,
时,当x∈[0,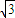 ]时,f(x)=3x-x3在[0,1]上单调递增,在[1,
]时,f(x)=3x-x3在[0,1]上单调递增,在[1,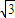 ]上单调递减,
]上单调递减,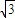 ,b]时,f(x)=x3-3x在[
,b]时,f(x)=x3-3x在[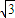 ,b]上单调递增,
,b]上单调递增,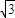 <b≤2时,在x=1时,f(x)取到最大值f(1)=2.
<b≤2时,在x=1时,f(x)取到最大值f(1)=2.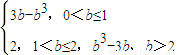 .
.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<