
分析 (1)求出函数的导数,可得切线的斜率,由点斜式方程可得切线的方程;
(2)求出函数的导数,令导数为0,可得极值点,分别计算极值和区间端点处的函数值,比较,即可得到所求最值.
解答 解:(1)函数y=$\frac{2}{3}$x3-2x2+3的导数为y′=2x2-4x,
可得在点(1,$\frac{5}{3}$)处的切线斜率为k=2-4=-2,
即有在点(1,$\frac{5}{3}$)处的切线方程为y-$\frac{5}{3}$=-2(x-1),
即为6x+3y-11=0;
(2)函数y=$\frac{2}{3}$x3-2x2+3的导数为y′=2x2-4x,
由y′=0,解得x=0或2,都在区间[-1,3]内,
由x=-1时,y=-$\frac{2}{3}$-2+3=$\frac{1}{3}$;
x=0时,y=3;x=2时,y=$\frac{16}{3}$-8+3=$\frac{1}{3}$;
x=3时,y=18-18+3=3.
则函数y在[-1,3]的最大值为3,最小值为$\frac{1}{3}$.
点评 本题考查导数的运用:求切线的方程和最值,考查化简整理的运算能力,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | -2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 150 | B. | 200 | C. | 500 | D. | 600 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
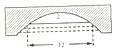 如图,一座圆弧形拱桥,当水面在如图所示的位置时,拱桥离水面2米,水面宽12米,当水面下降1米后,水面宽度为( )
如图,一座圆弧形拱桥,当水面在如图所示的位置时,拱桥离水面2米,水面宽12米,当水面下降1米后,水面宽度为( )| A. | 14米 | B. | 15米 | C. | $\sqrt{51}$米 | D. | $2\sqrt{51}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com