
分析 (1)建立单位圆,在单位圆中作出角,找出相应的单位圆上的点的坐标,由向量的数量积公式化简整理既得;
(2)与条件利用两个向量的数量积的定义求得ac=35,再利用余弦定理求得a2+c2=74,再根据a>c可得a和c的值.
解答 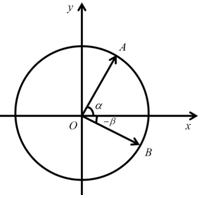 解:(1)证明:如图,在平面直角坐标系中,以原点为圆心,
解:(1)证明:如图,在平面直角坐标系中,以原点为圆心,
作一单位圆,再以原点为顶点,
x轴非负半轴为始边分别作角α,β.
设它们的终边分别交单位圆于点A(cosα,sinα),
B(cos(-β),sin(-β))
即有两单位向量$\overrightarrow{OA}$=(cosα,sinα),$\overrightarrow{OB}$=(cosβ,-sinβ),
∴$\overrightarrow{OA}$$•\overrightarrow{OB}$=cosαcosβ-sinαsinβ,
∵$\overrightarrow{OA}$$•\overrightarrow{OB}$=|$\overrightarrow{OA}$|•|$\overrightarrow{OB}$|•cos(α+β),且|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,
∴cos(α+β)=cosαcosβ-sinαsinβ
(2)∵$\overrightarrow{AB}\;•\;\overrightarrow{BC}=-\;\frac{65}{2}$,$cosB=\frac{13}{14}$,b=3.
∴$\overrightarrow{BA}$•$\overrightarrow{BC}$=$\frac{65}{2}$
∴accosB=$\frac{65}{2}$,
又cosβ=$\frac{13}{14}$,
∴ac=35
由余弦定理:cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{13}{14}$
∴a2+c2=74,由ac=35,a>c,
解得a=7,c=5.
点评 本题考查平面向量的综合应用,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,利用三角函数的性质合理地进行等价转化.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{4}$ | C. | $\frac{9}{4}$ | D. | $\frac{{2\sqrt{3}+6}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
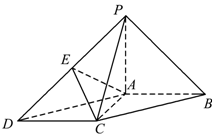 如图所示,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且 PA=AB=2,AC=1,点E是PD的中点.
如图所示,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且 PA=AB=2,AC=1,点E是PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow a$•$\overrightarrow b$-${\overrightarrow b^2}$=0 | B. | ${\overrightarrow a^2}-\overrightarrow a$•$\overrightarrow b$=0 | C. | $\overrightarrow a$⊥$\overrightarrow b$ | D. | $|{\overrightarrow a}|=|{\overrightarrow b}|$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{16}$ | B. | $\frac{7}{16}$ | C. | $\frac{9}{32}$ | D. | $\frac{23}{32}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .2 | B. | .-2 | C. | .3 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com