
| A. | $\overrightarrow a$•$\overrightarrow b$-${\overrightarrow b^2}$=0 | B. | ${\overrightarrow a^2}-\overrightarrow a$•$\overrightarrow b$=0 | C. | $\overrightarrow a$⊥$\overrightarrow b$ | D. | $|{\overrightarrow a}|=|{\overrightarrow b}|$ |
分析 两边平方得出关于x的恒等式,利用二次函数的性质得出不等式化简即可得出答案.
解答 解:∵$|{\overrightarrow a-x\overrightarrow b}|≥|{\overrightarrow a-\overrightarrow b}|$恒成立,
∴${\overrightarrow{a}}^{2}$-2x$\overrightarrow{a}•\overrightarrow{b}$+x2${\overrightarrow{b}}^{2}$≥${\overrightarrow{a}}^{2}$-2$\overrightarrow{a}•\overrightarrow{b}$+${\overrightarrow{b}}^{2}$恒成立,
即x2${\overrightarrow{b}}^{2}$-2$\overrightarrow{a}•\overrightarrow{b}$x-${\overrightarrow{b}}^{2}$+2$\overrightarrow{a}•\overrightarrow{b}$≥0恒成立,
∴△=4($\overrightarrow{a}•\overrightarrow{b}$)2-4${\overrightarrow{b}}^{2}$(2$\overrightarrow{a}•\overrightarrow{b}$-${\overrightarrow{b}}^{2}$)≤0,
∴($\overrightarrow{a}•\overrightarrow{b}$)2-2$\overrightarrow{a}•\overrightarrow{b}$•${\overrightarrow{b}}^{2}$+${\overrightarrow{b}}^{4}$≤0,
即($\overrightarrow{a}•\overrightarrow{b}$-${\overrightarrow{b}}^{2}$)2≤0,
∴$\overrightarrow{a}•\overrightarrow{b}$=${\overrightarrow{b}}^{2}$.
故选A.
点评 本题考查了平面向量的数量积运算,一元二次不等式的解法,属于中档题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{8}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
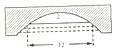 如图,一座圆弧形拱桥,当水面在如图所示的位置时,拱桥离水面2米,水面宽12米,当水面下降1米后,水面宽度为( )
如图,一座圆弧形拱桥,当水面在如图所示的位置时,拱桥离水面2米,水面宽12米,当水面下降1米后,水面宽度为( )| A. | 14米 | B. | 15米 | C. | $\sqrt{51}$米 | D. | $2\sqrt{51}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{35}{16}$ | B. | $\frac{35}{8}$ | C. | $\frac{35}{4}$ | D. | 105 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com