
| A. | $\frac{{\sqrt{3}}}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{8}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
分析 由题意知本题是一个几何概型,根据所给的条件很容易做出试验发生包含的事件对应的面积,而满足条件的事件是函数f(x)=$\frac{1}{2}$x3+ax-b在区间[-1,1]上有且仅有一个零点,求出导函数,看出函数是一个增函数,有零点等价于在自变量区间的两个端点处函数值符号相反,得到条件,做出面积,根据几何概型概率公式得到结果.
解答 解:由题意知本题是一个几何概型,
∵a∈[0,1],
∴f'(x)=1.5x2+a≥0,
∴f(x)是增函数若在[-1,1]有且仅有一个零点,则f(-1)•f(1)≤0
∴(-0.5-a-b)(0.5+a-b)≤0,即(0.5+a+b)(0.5+a-b)≥0,
a看作自变量x,b看作函数y,
由线性规划内容知全部事件的面积为1×1=1,满足条件的面积为$\frac{7}{8}$,
∴概率为$\frac{\frac{7}{8}}{1}$=$\frac{7}{8}$,
故选:C.
点评 本题是一个几何概型,对于这样的问题,一般要通过把试验发生包含的事件同集合结合起来,根据集合对应的图形做出面积,用面积的比值得到结果.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
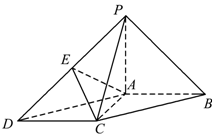 如图所示,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且 PA=AB=2,AC=1,点E是PD的中点.
如图所示,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且 PA=AB=2,AC=1,点E是PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow a$•$\overrightarrow b$-${\overrightarrow b^2}$=0 | B. | ${\overrightarrow a^2}-\overrightarrow a$•$\overrightarrow b$=0 | C. | $\overrightarrow a$⊥$\overrightarrow b$ | D. | $|{\overrightarrow a}|=|{\overrightarrow b}|$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com