
分析 (1)利用余弦定理转化求解即可.
(2)通过两角和与差的三角函数化简函数的解析式,通过B的范围,求解函数的最值即可.
解答 解:(1)由题意得,b2+c2-a2=bc
则$cosA=\frac{{{b^2}+{c^2}-{a^2}}}{2bc}=\frac{1}{2}$,且A∈(0,π),所以$A=\frac{π}{3}$.
(2)原式化为$y=2sin(B+\frac{π}{6})$,$B∈(0,\frac{2π}{3})$$B+\frac{π}{6}∈(\frac{π}{6},\frac{5π}{6})$,$sin(B+\frac{π}{6})∈(\frac{1}{2},\left.1]$,
故值域为(1,2].
点评 本题考查余弦定理的应用,两角和与差的三角函数,三角函数的最值的求法,考查计算能力.


 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{8}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
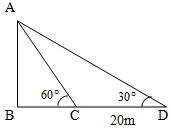 如图所示,为测量一水塔AB的高度,在C处测得塔顶的仰角为60°,后退20米到达D处测得塔顶的仰角为30°,则水塔的高度为$10\sqrt{3}$米.
如图所示,为测量一水塔AB的高度,在C处测得塔顶的仰角为60°,后退20米到达D处测得塔顶的仰角为30°,则水塔的高度为$10\sqrt{3}$米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
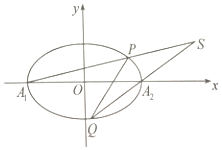 已知椭圆C的离心率为$e=\frac{{\sqrt{2}}}{2}$,长轴的左、右端点分别为A1(-2,0),A2(-2,0).
已知椭圆C的离心率为$e=\frac{{\sqrt{2}}}{2}$,长轴的左、右端点分别为A1(-2,0),A2(-2,0).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{35}{16}$ | B. | $\frac{35}{8}$ | C. | $\frac{35}{4}$ | D. | 105 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com