
分析 (1)根据题意,填写关于x、y的表格即可;
(2)由题意计算$\overline{x}$、$\overline{y}$与回归系数,写出回归方程,
利用回归方程预测老张孙子的身高.
解答 解:(1)根据题意,填表如下;
| x | 173 | 170 | 176 |
| y | 170 | 176 | 182 |
点评 本题考查了线性回归方程的求法与应用问题,是基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| 第1行 | 1 |
| 第2行 | 2 3 |
| 第3行 | 4 5 6 7 |
| … | … |
| A. | 263 | B. | 505 | C. | 519 | D. | 530 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 150 | B. | 200 | C. | 500 | D. | 600 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{8}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
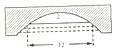 如图,一座圆弧形拱桥,当水面在如图所示的位置时,拱桥离水面2米,水面宽12米,当水面下降1米后,水面宽度为( )
如图,一座圆弧形拱桥,当水面在如图所示的位置时,拱桥离水面2米,水面宽12米,当水面下降1米后,水面宽度为( )| A. | 14米 | B. | 15米 | C. | $\sqrt{51}$米 | D. | $2\sqrt{51}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com